100 45

Jefli przyjmiemy założenie • <r, * a₃ * <r_s, to równanie (3.33a) możemy podzielić stronami przez 2 (<rj — <r₃), zaś równanie (3.33b) przez 2(<r_a—<r₃). Otrzymamy

+^<T$)^<*wt — 2£(<r_ł—a₃)a*, +(<r₂—er₃)a*_a+e₃]a,i — 0,    (3.34a)

(c₂+'3)^2-2[(ffj    +(<r₂    +^3]*.2 - 0 .    (3.34b)

Przed przystąpieniem do rozwiązania tego układu równań algebraicznych ze względu na a,, i a,, zwrócimy uwagę na:

—    banalność rozwiązania a,₃ *= o,₂ *= 0; daje to bowiem a_r3 = ± 1, a więc wersory •(0,0, ±1); wersory te wyznaczają płaszczyznę główną, prostopadłą do osi 3, dla której wektor naprężenia jest prostopadły do płaszczyzny, a zatem t, = 0;

—    nieistnienie rozwiązania er,, 9* 0, o,₂ ł* 0; odejmując bowiem stronami równania (334) otrzymujemy równość <r_t — <x₃ = 0, co wobec założenia o, 9* <r₂ jest niemożliwe. Rozwiązania, które nas będą interesować mogą być zatem następujące:

a,_t — 0, a,₂ 9* 0 oraz a,_x 7* 0, a_r2 = 0 .

W pierwszym przypadku równanie (3 J4a) jest spełnione tożsamościowo, z drugiego zaś równania po podzieleniu przez a,₂ otrzymujemy równanie

1 -2*l_x - 0,

którego pierwiastkami są «,₂ — ±—Wykorzystując warunek poboczny (332) otrzy-

v²

m ujemy współrzędne wersorów płaszczyzn

0,1 - 0, a,_;

0,3

^±V²*

(335)

W punktach przecięcia bryły tymi płaszczyznami możemy spodziewać się ekstremum ftinkcji r,.

W drugim przypadku rozwiązanie układu (334) po wykorzystaniu (3.22) jest:

1

fi#

a;* 10.    a,3 = ±

1

V²*

(3.36)

Gdybyśmy a zależności (331) wyeliminowali inną zmienną niż a,₃, np. a_0l wyrazili poprzez er,2 i 0,3, i powtórzyli tok postępowania, otrzymalibyśmy jeszcze jedno rozwiązanie

1

0*2

1

= 0.

(3.37)

Reasumując, dla płaszczyzn określonych wersorami o współrzędnych (3.35), (3.36) i (337) spodziewać się możemy ekstremum funkcji x\. Nie będziemy tu przytaczać warunku

| Zalecamy czytelnikowi przeprowadzenie dalszej ąralizy dla przypadku o_t y* o_t ■■ 0% oraz podanie odpowiedzi, dlaczego w przypadku o, = a, «= a_t analiza jest natychmiastowa.

wystarczającego, który pokazałby, te funkcja (3.31) przyjmuje na podanych ptaazczyzaaeli swoje maksima lokalne. Wartości maksymalnych naprężeń stycznych otrzyaaay podstawiając kolejno (3.35), (3.36) i (3.37) do (3.31). Otrzymujemy odpowiednio

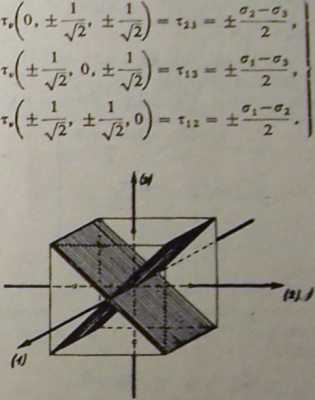
Rys. 3.13

(33g)

Na rysunku 3.13 pokazano płaszczyzny określone wessorami o współrzędnych (335), na których t, = r₂₃. Nietrudno narysować pozostałe płaszczyzny wyznaczone wena-rami o współrzędnych (3.36) i (337). Stwierdzimy wtedy, że płaszczyzny, którym przyporządkowane są ekstremalne naprężenia styczne, przechodzą przez jedną z oa głównych i do pozostałych są nachylone pod kątem 45*.

1.11. Nierówności 1 kola Mokra

Pewne zagadnienia z analizy stanu naprężenia można wykonać graficznie wykorzystując kola Mohra. Niezależnie od tego, że konstruowanie kół Mohra jest doskonałym ćwiczeniem poznanej analizy, to w późniejszych studiach teorii plastyczności konstrukcję tę będziemy wykorzystywać. Pierwsze zadanie jakie sobie postawimy, to określenie zbioru rozwiązań (<r„ t,) dla dowolnych płaszczyzn przekroju bryły, przechodzących przez ustalony punkt, w którym dana jest macierz naprężeń, określona w układzie osi głównych. ^ Przypomnijmy, że zgodnie z przyjętymi oznaczeniami w punkcie 13 <r, jest miarą rantu