100B96

10. Wybrane zagadnienia geometrii wykreślnej

10. Wybrane zagadnienia geometrii wykreślnej

! | WyfcrtłJawr okręgu opisanego na trójkącie

B

■

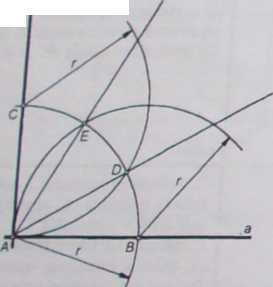
Podział kąta prostego na 3 równe części *1

Podział okręgu na n równych części

cd. tabl. 10.1

Wyznacza się symelralne boków trójkąta AB, BC i CA. Punkt ich przecięcia jest | szukanym środkiem O okręgu opisanego na j danym trójkącie.

Zakreśla się z wierzchołka A łuk o promieniu r, otrzymuje się punkty B i C, z których tym samym promieniem r zakreśla się dwa tuki wyznaczające punkty D i E. Proste AD i AE dzielą kąt prosty na 3 równe części.

Na osi symetrii AB oznacza się środek O i kreśli się okrąg o promieniu OA. Z punktów A i B rysuje się luki pomocnicze w celu wykreślenia prostopadłej CD (drugiej osi symetrii) do prostej AB. Średnicę AB dzieli się na tyle części, na ile chce się podzielić okrąg. Otrzymany odcinek x odkłada się na osi pionowej z punktu C i poziomej z punktu B. Otrzymane punkty E i F łączy się prostą. Z punktu G prowadzi się prostą do I punktu 3’. Odcinek G3‘ jest szukanym bokiem wieloboku foremnego. Punkt C | łączy się zawsze z końcem trzeciego odcinka bez względu na liczbę boków j wielokąta.

0 u/yhrane zagadnienia geometrii wykreślnej ' '

cd. tabl. 10.1

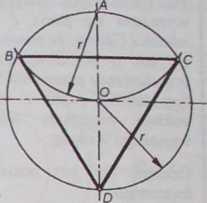
podział okręgu na 3 części

Podział okręgu na 6 części

Po narysowaniu okręgu o promieniu OA = r i osi symetrii z punktu A zakreśla się luk kołowy o promieniu r. W ten sposób znajduje się punkty B i C stanowiące dwa wierzchołki trójkąta. Łącząc punkty B,C '\D otrzymuje się trójkąt foremny wpisany w dany okrąg.

Po narysowaniu okręgu o promieniu O A = r i osi symetrii z punktów A i D zakreśla się łuk kołowy o promieniu r. W ten sposób znajduje się punkty B i C oraz E i F | stanowiące wierzchołki sześciokąta foremnego wpisanego w okrąg.

Podział okręgu na 4 części

Konstrukcję opiera się na punktach przecięcia się okręgu z osiami symetrii.

Podział okręgu na 8 części

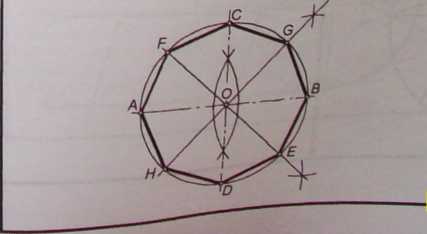
Ośmiokąt foremny opiera się na punktach przecięcia się okręgu z osiami symetrii oraz dodatkowo na wykreślonych dwóch dwusiecznych kątów prostych utworzonych z osi symetrii okręgu.

aul

■

___ i