100B99

10. Wybrane zagadnienia geometrii wyir,.*^

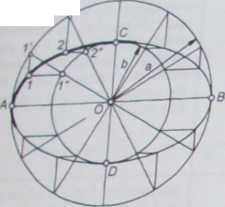
Wykreślanie elipsy o osiach 2a i 2b

■ zA

Wykreśla się promieniach

_cd. tabl Ir)

'■'STrr'-

Następnie ze środka O prowadzi _sie promieni przecinających ^ę P?k odpowiednio w punktach /• 2‘    °- ^El

Z punktów 1\ 2'

■ i r

proste równolegle do małej osi dj_psy l ^SIę punktów 2" proste równoleełe !,* dużej osi elipsy o. Punkty przecięcia tych są punktami wykreślanej

prostych /, 2 elipsy.

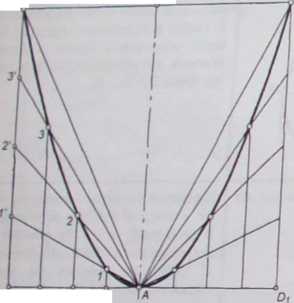
Wykreślanie paraboli

C    J

Ct r r r

Wykreślanie hiperboli

Mając oś paraboli AE i jej cięciwę CD rysuje się prostokąt CDD,C,. Następnie odcinki ACi (AD,) oraz CC, (DD,) dzieli się na tę samą liczbę równych części. Proste AJ A2 ... w przecięciu z odpowiednimi prostymi prostopadłymi do C,D poprowadzonymi z punktów l", 2", ... dają szukane punkty /, 2, ... wykreślanej paraboli.

Dla danych dwóch asymptot a i b oraz jednego punktu hiperboli H wykreśla się proste / i m równoległe do asymptot a i b przez punkt H. Następnie z punktu przecięcia się asymptot O prowadzi się wiązkę prostych, które przecinają się z prostymi / i m, wyznaczając punkty / , 2', ... i I", 2". ... . Z punktów tych rysuje się odpowiednie równoległe do asymptot a i b, otrzymując w przecięciu punkty I, 2, wykreślanej hiperboli.

i

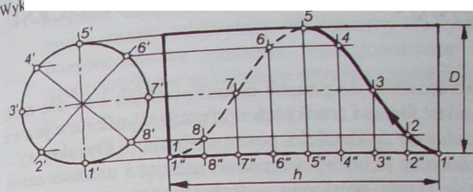
Na narysowanym w dwóch rzutach walcu o średnicy D i długości h (skoku gwintu) dokonuje się podziału powstałego okręgu w rzucie z boku oraz długości walca w rzucie z przodu na jednakową liczbę części (np. 8). Następnie prowadzi się z punktów 12\ ... proste poziome, a z punktów 1", 2”, .. proste pionowe. Punkty 1, 2, ... przecięcia się odpowiednich prostych są punktami wykreślanej linii śrubowej.

,0

_lanie linii śrutx>^wcj ^{0 śrct}.ⁿ'^cy ^ i ^s'^c0*^cu h

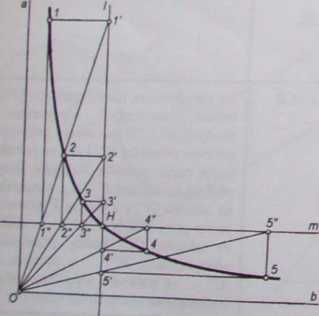
"^Sianie zarysu ewolwentowego	Ewolwentę otrzymuje się przetaczając prostą bez poślizgu po okręgu o średnicy d,.
	Punkt na tej prostej kreśli zarys
	ewolwentowy.
, g- r 6- g*	Kreśli się koło zasadnicze o średnicy dT, na którym odkłada się jednakowe łuki zaczynając od punktu A. Środek okręgu O łączy się prostymi z punktami 1\ 2\ ... i wykreśla się linie do nich prostopadłe (styczne do okręgu) o kierunkach 17, 2 ’2,... . Na pomocniczej prostej m odkłada się długości rozwiniętego tuku, a następnie odcinek Al" odkłada się na prostej I 7 z punktu 1odcinek A2" na prostej 27 z punktu 2’ itd. Otrzymane punkty I, 2, .
/ \
	tworzą zarys ewolwentowy.

■