1 7c pole sil potencjalnych

Ima znak ujemny — wykonuje ją pole sil kosztem energii zgromadzonej w podniesionym cięża-rzc — energii potencjalnej. Energia, bardzo ważna wielkość fizyczna, jest pnirą zgromadzoną lub zdolności.) pola sił do wykonania pracy Podnoszony ciężar będzie miał w każdym punkcie “przestrzeni energię zależną od położenia, proporcjonalną cło masy podnoszonego obiektu. Jeśli więc podzielimy energię prac/ rna.se obiektu, to otrzymamy nnlr skalarne charakteryzujące pole sił zachowawczych, już nienależne od etyli obiekt.u, którym posłużyliśmy się; w badaniach pola (obiektu próbnego) Ta cechą nazywa się potencjałem pola Wiemy również, że także sita działająca na masę próbną jest do tej masy proporcjonalna i stosunek sił)' ciężkości do masy ciała jcst^cechą wektorową eharakteryzującą pole. Mówimy że ten stosunek F/m - g jest natężeniem iHtlu.grawitacyjnego i^nazywą się przyspieszeniem grawitacyjnym. W niewielkich odległościach od powierzchni Ziemi, w których odbywa się zwykle nasza ludzka działalność, siła jest określona wzorem\F = my ^ energia potencjalna wzorem! E„ - mgh \

Fnergia rnoże być gromadzona nie tylko w położeniu obiektu w polu zachowawczym czyli potencjalnym ale także w stanic ruchu ciała. Praca rozpędzania ciała od prędkości zerowej

d W - Fdr

(2.22)

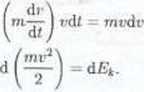
Wielkość

I nazywamy energią kitiofyr-yrj^ i

Wróćmy do niezależności pracy w polu zachowawczym od drogi. Załóżmy, że pracę wykonuje układ pole-ciężar.

Musi istnieć taka funkcja U. której

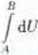
= Ub-U_a.

(2.23)

Różniczka tej funkcji trzech zmiennych nazywa się

... dU ,    <X7 QU,

^d!' iz^Ax+—.ⁱy+ ar^dj

0x &y

Podobnie rozłożony na składowe wyrażenie F • dr

(2.24)

(2.25)

F - dr F_J:drr + F_vdy -f Rdz.

Dla spełnienia zasady zachowania energii założę, że kiedy układ wykonuje pracę to jego cne.rgia zmniejsza się

-dV = F • dr.    (2.26)

Przyrównam poprzednie rozwinięcia

(OU . _t i)b\ dU \

= F_t dx + F,dy + Fgdz.    (2.27)

20