114 115

I 14 Programowanie liniowe całkowitoliczbowe

Otrzymujemy następujące zadania:

I 14 Programowanie liniowe całkowitoliczbowe

Zadanie 4

3xj + 3x2+ 13x₃ —> max, - 3x, + 6x₂ + 7x₃ < 8,

6x, - 3x₂ + 7x₃ < 8,

x, >0,

0«x₂<2,

0<x₃<0.

Zadanie 5

3x, + 3x₂ + 1 3x₃ —» max, — 3x, + 6x₂ + 7x₃ ^ 8,

ÓX| —3x₂ + 7x₃ <8, x, > 0,

0<x₂<2,

1 <x₃ < 5.

Znajdujemy rozwiązania powyższych zadań. Zadanie 4 ma rozwiązanie: x, = 2,333, x₂ = 2, x₃ = 0 i speinia warunki całko w i toliczbowości, pomimo że x, nie jest całkowite (ale nie wymagamy tego). Optymalna wartość funkcji celu wynosi 13.

Dla zadania 5 mamy: x, =0,333, x₂ = 0,333, x₃=l.

Optymalna wartość funkcji celu wynosi 15.

Iteracja 3

Na liście zadań znajdują się obecnie: zadanie 2, zadanie 4 i zadanie 5. Ponieważ zadanie 2 zostało już uprzednio podzielone, usuwamy je z listy. Pomimo że rozwiązanie zadania 4 speinia wszystkie warunki całkowitoliczbowości, nie możemy jeszcze zakończyć obliczeń, gdyż może się zdarzyć, że dalszy podział zadania 5, dla którego otrzymano lepszą wartość funkcji celu, wygeneruje rozwiązanie, które będzie lepsze od rozwiązania zadania 4. Do dalszego podziału wykorzystamy więc zadanie 5. Zmienna x₂ w rozwiązaniu zadania 5 nie spełnia warunków całkowitoliczbowości, dlatego też dokonamy kolejnego podziału ze względu na tę zmienną (rys. 2.10).

Otrzymujemy: Zadanie 6

3x, + 3x₂ + 1 3x₃ —> max, — 3xi + 6x₂ + 7x₃ < 8,

ÓX| - 3x₂ + 7a'₃ < 8,

x, >0,

0 ^ x₂ < 0,

Zadanie 7

3xi + 3x₂+ I3x₃ —> ntax, — 3x, + 6x₂ + 7x₃ < 8,

ÓX| — 3x₂ + 7x₃ < 8,

X, 0,

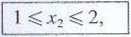
Rysunek 2.10

_i_4_

0 0,333    1    2    *2

Zadanie 6 ma rozwiązanie: jc, =0, .r₂ = 0, x₃ = 1,143.

Optymalna wartość funkcji celu wynosi 14,857. Zadanie 7 jest sprzeczne. Iteracja 4

Porządkujemy listę zadań. Na liście zadań mamy: zadanie 4, zadanie 5, zadanie 6 i zadanie 7. Zadanie 5 usuwamy z listy ze względu na to, że zostało już podzielone. Usuwamy również zadanie 7, które jest sprzeczne. Pozostaje zadanie 4, którego rozwiązanie spełnia warunki całkowitoliczbowości, ale wartość funkcji celu jest gorsza niż dla zadania 6. Podobnie jak w iteracji 3, nic możemy jeszcze zakończyć rozwiązywania zadania, gdyż wciąż istnieje możliwość wygenerowania rozwiązania lepszego od tego, które uzyskaliśmy przez rozwiązanie zadania 4. Do dalszego podziału wybieramy zadanie 6. Dokonamy podziału tego zadania ze względu na zmienną x₃ (rys. 2.11).

Rysunek 2.1 I

—U_i

1 1,143    2

Otrzymujemy:

Zadanie 9

3x, +3x2+ 13x₃ —> max, - 3x, + 6x₂ + 7x₃ < 8,

6x, - 3x₂ + 7x₃ ^ 8, x, » 0,

0s$x₂<0,

2<x₃«5.

Zadanie 8

3xi + 3x₂ + I3x, —> i - 3jT| + 6x₂ + 7x₃ < 8,

6x, — 3x₂ + 7x₃ < 8,

>0,

0s$x₂<0,

1 I.

Rozwiązując zadanie 8, mamy:

-*i = 0,167, x₂ = 0, X; = 1.

Optymalna wartość funkcji celu wynosi 13,500. Zadanie 9 jest sprzeczne.