139(1)

Jeśli x wzrośnie o małą wielkość dx. to objętość V kuli wewnętrznej owiększy się o .J V, czyli o różnicę objętości kul o promieniach x i x+dx

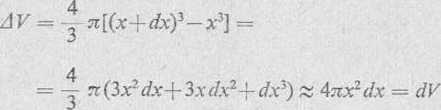
Zakładając, że we wszystkich punktach tej cienkiej powłoki kulistej o objętości dV gęstość nic zmienia się i wynosi kx, obliczamy przybliżoną wartość jej masy dm = kx dV = 4krcx^s dx.

Poszukiwaną masę m kuli o promieniu r otrzymamy całkując dm w granicach od x = 0 do x - r\ mamy

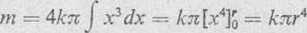
o

669.    Kwadrat o boku 8 m zanurzono pionowo w wodzie tak, że jeden jego boków leży' na powierzchni wody. Obliczyć napór (parcie wody)

na ten kwadrat oraz napór wywierany na każdą z części kwadratu, na które dzieli go przekątna.

670.    Zbiornik cylindryczny o osi poziomej i promieniu 3 dcm napełniono do połowy rtęcią (ciężar właściwy rtęci 13,6 G/cm³). Wyznaczyć napór, jaki wywiera rtęć na każdą z płaskich pionowych ścianek zbiornika.

671.    Obliczyć, jaką pracę należy wykonać, aby wypompować wodę zawartą w półkulistym zbiorniku o promieniu 2 m.

672.    Zbiornik cylindryczny o objętości 0,1 m³ napełniono powietrzem ^ pod ciśnieniem atmosferycznym, które rozpręża się, wypychając tłok

(w próżnię). Obliczyć pracę, jaką wykona powietrze, jeśli jego objętość zwiększy się do: 0,3 m³, 0,4 m³, 0,5 m³, a proces będzie przebiegał izoter-micznie (ciśnienie atmosferyczne wynosi 10 330 kG/m²).

673.    Przy warunkach podanych w poprzednim zadaniu, obliczyć pracę adiabatycznego rozprężania się gazu (powietrza).

674.    Stożek o wysokości 10 dcm i o średnicy podstawy 20 dcm zanurzono w' wodzie, przy czym oś stożka skierowana jest pionow o, a jego wierzchołek leży na powierzchni wody. Jaką pracę trzeba wykonać, aby wydobyć

I stożek z wody? Ciężar właściwy materiału, z którego stożek jest sporządzony

' wynosi 3 kG/dcm³

675.    Belka drewniana o wymiarach a = 6 m, b = 0,3 rn, c = 0,2 m i o ciężarze właściwym <5 = 0,8 G/cm³ jest zanurzona w wodzie. Jaką pracę należy wykonać, aby wydobyć ją z wody?

676.    Wiedząc o tym, że wydłużenie sprężyny jest proporcjonalne do przyłożonej siły rozciągającej, wyznaczyć pracę, jaką należy zużyć, aby rozciągnąć sprężynę o 4 cm, jeśli na rozciągnięcie jej o 1 cm trzeba użyć siły równej 3 kG.

' 677. Cysternę cylindryczną o osi poziomej, mającej wysokość H i promień podstawy i?, napełniono wodą. Obliczyć, w ciągu jakiego czasu przez otwór w dnie o przekroju S będzie opróżniona: 1) górna połowa cysterny, 2) dolna jej połowa¹⁵.

678.    Jaka ilość wody przepływa w ciągu 1 sek przez prostokątne ujście w pionowej tamie, jeśli wiadomo, że jego głębokość wynosi h, a szerokość a‘>.

679.    Gęstość stożka prostego, o wysokości H i kącie między tworzącą a wysokością równym a, w każdym jego punkcie jest wprost proporcjonalna do odległości tego punktu od płaszczyzny przechodzącej przez jego wierzchołek równolegle do podstawy. Obliczyć masę stożka.

§ 9. Współrzędne środka ciężkości

Środkiem ciężkości zbioru punktów materialnych nazywamy punkt przyłożenia wypadkowej równoległych sił ciężkości, przyłożonych w tych punktach.

Dla łuku materialnego AB krzywej płaskiej współrzędne prostokątne środka ciężkości C są określone wzorami

m_x

m

0)

m_y

^Xc m

(B)

/ d(M)xdl

(A)_

(8) '■

f 3(M)dł

(A)

<8>

/ ó(M)ydl

(/O    _

(8)

f KM) dl

w

gdzie: m — masa łuku AB, m_x i m, — momenty statyczne łuku względem osi Ox i Oy, S(M) — gęstość liniowa rozkładu masy w punkcie M(x,y) łuku, dl — różniczka długości łuku, a (A) i (B) — wartości obranej zmiennej całkowania w punktach końcowych A i B.

W przypadku gdy łuk materialny jest jednorodny, wzory (1) upraszczają się, gdyż stałą <5 można wtedy wynieść przed znaki całek.

') Patrz zad. 666.

231