180 3

356

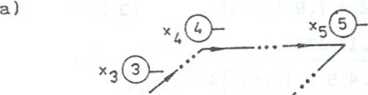
3.125 a nazwano go układem sterującym). Po rozładowaniu w punkcie wyładowczym wózki ustawiają się na początku trasy.

356

b)

wózki wyładowczy

Liczba ładunków 8 *1 ,-V>	Liczba wózków (w NKB) ^W1^W2^W3
0	0 0 0
1.2	0 0 1
3,4	0 1 0
5,6	0 1 1
7.8	1 0 0

sumowanie arytme

tyczne

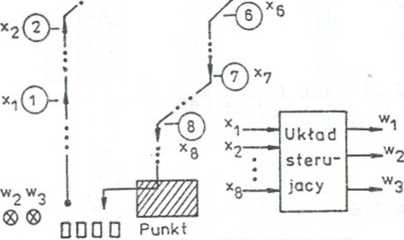
Rys.3.125. Struktura problemu z przykładu 3.64 Rozwiązanie

Wejściami układu sterującego są stany sygnałów zgłoszenia x,, y-2< ■ • •. Xg. natomiast jego wyjściami - trzy bity Wj, Wg, w„ liczby wózków, które należy wysłać na trasę. Ponieważ aktualny stan wyjść układu sterującego jest funkcją wyłącznie aktualnego stanu jego wejść, mamy tu do czynienia z układem kombinacyjnym. Opisuje go zespół trzech funkcji ośmiu zmiennych:

Wj = f j ( Xj,x₂.....Xg), j= 1.2.3. (3.246)

, Ze względu na dużą liczbę wejść układu oraz fakt, że zasadnicza jego część “zajmuje się” zliczaniem sygnałów zgłoszeń a zatem wykonuje - w odniesieniu do kolejnych wejść x.- analogiczne czynności, rozsądna jest realizacja tego układu jako układu iteracyjnego (rys. 3.126).

Wektor przeniesienia P^ oznacza liczbę zgłoszonych ładunków z pierwszych "i" punktów załadowczych. Ponieważ zarówno w przypadku zgłoszenia siedmiu jak i ośmiu ładunków należy wysłać na trasę cztery wózki, wektor P. można zakodować na trzech bitach (p.,q., r^) - rys.

3. 127 a.

^X1 ^x2

	^P1	—^v ■"]	^P2	^Pi-1	. i	^pi	^P7	8	^PR	U.
1	p=>	2	> ’			=> •			P=>	pom.

Rys. 3.126. Struktura układu sterującego z przykładu 3.64

a)

b)

^pi	Pi^i^ri	^ri-K
		0	0	1
0	0 0 0	1	1	2
1	o O	2	2	3
2	0 1 0	3	3	4
3	0 1 1	4	4	5
4	1 0 0	5	5	6
5	1 0 1	6	6	7
6	1 1 0	7	7	7
7 i 8	1 1 1			^Pi

Rys. 3.127. a) sposób kodowania wektora ; b) zasada działania i-tego bloku, i=2,3,...,8 z rys. 3.126

Na rys. 3.127 b przedstawiono opis działania i-tego bloku z rys. 3. 126 dla i = 2,3,..,8, przy czym wektory Pj_j i Pj zapisano dziesiętnie. Przechodząc na ich binarną reprezentację z rys. 3.127 a, tabelę z rys. 3.127 b można przetransformować na trzy tabele Karnauhga przedstawione na rys. 3.128.