196 197

196

Metody wielokryterialne

Rysunek 4.4

y₂

Punkty

nieporównywalne z Y'

Stożek ocen dominujących nad Y'

Punkty

nieporównywalne z Y'

Stożek ocen

zdominowanych przez Y'

Rysunek 4.5

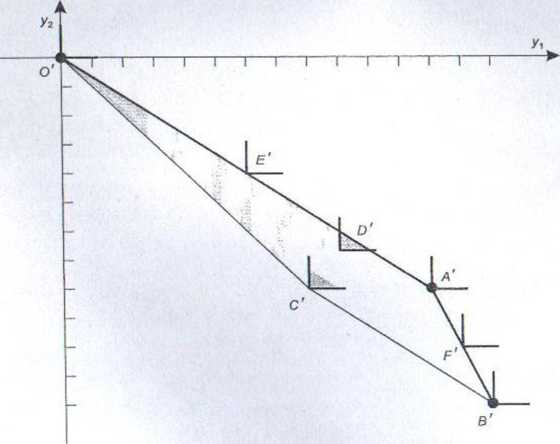
Metoda geometryczna znajdowania rozwiązań niezdominowanych została przedstawiona na rys. 4.5. Punkty OA', B\ E' i F ilustrują wybrane rozwiązania niezdominowane, natomiast C' i Z)' — niektóre rozwiązania zdominowane. Rozwiązania niezdominowane to te, które znajdują się na odcinkach O' i A' oraz A' i B'. Tak więc marny trzy niezdominowane wierzchołki oraz nieskończenie wiele rozwiązań niezdominowanych, które nie są wierzchołkami.

Przedstawione powyżej rozważania geometryczne ilustrują kolejne twierdzenie, które ma zastosowanie w przypadku zadań wielokryterialnego programowania liniowego.

Twierdzenie 4.2

W zadaniach wielokryterialnego programowania liniowego rozwiązania niezdominowane zawierają się w brzegu zbioru rozwiązań dopuszczalnych w przestrzeni kryterialnej. Żaden punkt wewnętrzny tego zbioru nie może być punktem niezdominowanym.

Rozwiązania w przestrzeni decyzyjnej, odpowiadające rozwiązaniom niezdominowanym w przestrzeni kryterialnej, nazywamy rozwiązaniami sprawnymi.

4.3. Metoda ADBASE

Metoda ADBASE (Adjacent Efficient Basis Procedurę) pozwala na wyznaczenie zbioru wszystkich bazowych rozwiązań sprawnych wielokryterialnego zadania programowania liniowego. Składa się ona z trzech faz:

—    wyznaczenia pierwszego bazowego rozwiązania dopuszczalnego,

—    wyznaczenia pierwszego rozwiązania sprawnego,

—    wyznaczenia pozostałych rozwiązań sprawnych.

Aby wyznaczyć pierwsze (a potem kolejne) bazowe rozwiązanie dopuszczalne, skonstruujemy rozszerzona tablicę simpleksową. Do wyznaczenia pierwszego rozwiązania bazowego wykorzystamy zadanie testujące. Pozostałe rozwiązania-bazowe uzyskamy, wykorzystując pewne dalsze własności bazowych rozwiązań sprawnych. Rozważania ograniczymy głównie do sytuacji, gdy zbiór rozwiązań dopuszczalnych rozpatrywanego zadania jest ograniczony.

Zazwyczaj liczba znalezionych bazowych rozwiązań sprawnych jest znaczna, dlatego też do wyboru rozwiązania końcowego wykorzystywanego przez decydenta do podjęcia decyzji stosuje się najczęściej dalsze procedury, przede wszystkim filtracji. Dokładny ich opis można znaleźć w innych podręcznikach¹.

1

W literaturze w języku polskim procedury filtracji opisane są w książce pod red. T. Trzaskalika, Metody wielokryterialne na polskim rynku finansowym, PWti, Warszawa 2006.