1tom073

4. INFORMATYKA 148

Poniżej podano kwadratury Gaussa, w których w zależności od przedziału [u, ł>] i funkcji wagowej węzły a, są pierwiastkami określonych wielomianów ortogonalnych i stale H_; są obliczane z odpowiednich równości.

Kwadratura Gaussa- I.egendrea z wagą W{x) = 1 w przedziale [—1,1] ma postać

j/(-x)dx= i HJW+E    (4.10)

-I    i= 1

gdzie: węzły a, (i = 1,2, ...,n) są zerami wielomianu Legendre’a, a H_i i E oblicza się ze wzorów

2    '7²"⁺¹ (n')¹

^z ..... - ' ’

H,=

(n+i)£„₊₁(a_i)L„(ćJ_£)

((= 1,2.....n) E =

(2n+ l)(2n/!)

-tP²"Xn)

(r/ leży w przedziale [— 1,1]).

Tablica 4.8. Zera wielomianów Legendre’a i współczynniki kwadratury Gaussa-Legendre’a

n	Węzły Oj	Współczynniki H,
2	±0,577350 = ± 1A/3	1
3	0	8/9
	+0,774597	5/9
4	+0,339981	0,652145
	+0,861136	0,347855
5	0	0,568889
	+0,538469	0,478629
	±0.906180	0/236927

W tablicy 4.8 podano zera wielomianów Legendre'a i współczynniki H, dla n = 2,3,4, 5. Wielomiany Legendre’a można obliczać ze wzoru rekurencyjncgo.

Przykład 4.3. Stosując kwadraturę Gaussa-Legendre’a dla n = 4, obliczyć całkę

i

J e*dx -1

Znaleźć oszacowanie błędu tego przybliżenia. Posługując sic tabl. 4.8 dla n = 4, oblicza się

j _e*dx = 0,652145-e^0,339981 + 0,652145-e⁰-³³⁹⁹⁸¹ + 0,347855-e°-^86łł38 + 0,34 7 8 55 e °'^8bn30 = 2,35040196 -1

Dokładna wartość całki jest równa e - — = 2,35040238. Błąd metody wynosi

e

•c'¹ = 2,8-10 ⁷-e’

E = -

2⁹-(4!)⁴

9 - (8!)³

przy czym tj — leży w przedziale (-1,1). Stąd oszacowanie 10"⁷ w2,810-⁷-e-¹ <£<2,8-10 ⁷-e fi? 7,8-10"⁷

Kwadratura Gaussa-Laguerre’a z wagą W(x) = e ^x w przedziale (0, oc) ma postać | e~^xf(x)dx = £ H_if(a_i) + E

0    i= 1

PM) =

gdzie węzły a,(i = 1,2,...,«) są zerami wielomianu Laguerre’a d

dx”

natomiast współczynniki H_i oraz błąd E oblicza się ze wzorów ⁽"^!> (i = 1,2,..., n); E =-^-f⁽²">(,

/ł,=

(2 nf

gdzie ii — leży w przedziale [0, oo].

W tablicy 4.9 podano zera wielomianów Laguerre’a i współczynniki H_t kwadratury Gaussa-Lagucrrc’a dla n = 2,3,4,5. Wielomiany Laguerre’a najłatwiej obliczać ze wzoru

rekurencyjnego

P„+i(x) = (1 +2n—x)P„(x)—n²P_ll__l(x) (n > 1)

Tablica 4.9. Zera wielomianów Laguerre*a i współczynniki kwadratury Gaussa-Laguerre’a

n	Węzły a{	Współczynniki Hf	n	Węzły a.	Współczynniki Hf
2	0,585786	0,853553		4.536620	0,038888
	3,414214	0,146447		9,395071	0,000539
3	0.415775	0,711093	5	0,263560	0,521756
	2,294280	0,278518		1,413403	0,398667
	6,289945	0,010389		3.596426	0,075942
4	0,322548	0,603154		7.085810	0,003612
	1,745761	0,357419		12,640801	0,000023

Przykład 4.4. Obliczyć całkę J (2e)'*dx

i

stosując kwadraturę Gaussa-Laguerre’a dla n — 4. Oszacować błąd przybliżenia.

Z tablicy 4.9 odczytuje się współczynniki H_} i węzły dla n = 4; zatem

J (2e)"*dx« Je ^x(~] dx * 0,603154-2 °-^32254ft+ 0,357419•2-^,•^,4576,+0,038888-2^-4'⁵³⁶⁶²+ 0,000539 x o    o \2/

x 2"^9,395071 =0,48231591+0,10657398 + 0,00167554 + 0,0000008 = 0,59056623 Błąd wyraża się wzorem

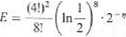
gdzie 11 leży w przedziale (0, zo). natomiast 2 " można dla rj należącego do przedziału (0, oc) oszacować następująco: 0 < 2 " < 1. Stąd

(4?)- / i V

0<£< — In- 35 0.00076121

8! V 2)

Kwadratura Gaussa-Her mi te'a z wagą W(x) — e ^x‘ w przedziale ( — co, oc) ma postać

«C    _n

I e-*7(x)dx= X HJ(a_t)+E

-CO    i= 1

gdzie węzły a_f (i =1,2,..., n) są zerami wielomianu Hermitc’a

dxⁿ

^{a Ws}półczynniki H_i i błąd E są dane wzorami

nL/Jt ,

E = ^—f²ⁿ\v)

ⁿ(2n)V

r,    2ⁿ⁺ⁱn\Jn

~ 77--- (i = 1,2,.... ń);

H_{n + l}(_ai)HM)

Ptzy czym t] — leży w przedziale [—oc, oo].