214 215

214 Metody wielokryterialne

4.4.5. Wykorzystanie punktu idealnego

Generując w punkcie 4.4.1 rozwiązania sprawne za pomocą jednej funkcji celu, rozwiązywaliśmy kolejne zadania 2, dla / = 1, ..., m, gdzie w oznacza liczbę rozpatrywanych kryteriów. Oznaczymy przez y° optymalną wartość funkcji celu, otrzymaną z rozwiązania zadania Z,. W przestrzeni kryterialnej możemy określić punki Y (y*, .... nazywany rozwiązaniem idealnym. Punktowi temu zazwyczaj nie odpowiada w przestrzeni decyzyjnej żadne rozwiązanie dopuszczalne. Pomimo \ to w przestrzeni kryterialnej może być on wykorzystany przez decydenta jako punkt i odniesienia w stosunku do tych rozwiązań, które są dla niego osiągalne.

Określając — w odpowiadający rozpatrywanemu problemowi sposób — odległość między punktami w przestrzeni kryterialnej, można szukać takiego rozwiązania, które jest położone najbliżej punktu idealnego. Przy odpowiednim określeniu sposobu mierzenia odległości między punktami otrzymujemy rozwiązanie sprawne. Geometrycznie sposób takiego postępowania ilustruje kolejny przykład. Otrzymujemy w ten sposób zadanie programowania kompromisowego.

Przykład 4.9

Wykorzystamy podejście programowania kompromisowego do wyznaczenia rozwiązania sformułowanego w przykładzie 4.2, przyjmując metrykę euklidesową jako sposób mierzenia odległości w przestrzeni kryterialnej.

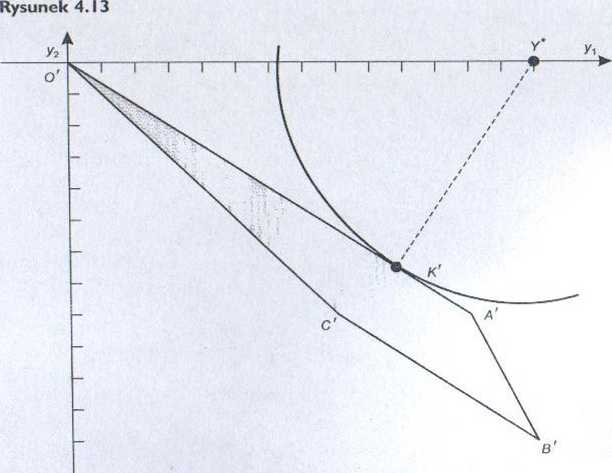
Rozwiązując zadania Z, i Z, (przykład 4.4), znaleźliśmy jednocześnie składowe rozwiązania idealnego w przestrzeni kryterialnej, które są następujące: =14, yl = 0, stąd V'*( 14, 0). Zaznaczamy punkt Z' i znajdujemy taki okrąg

0    najmniejszym promieniu, który ma dokładnie jeden punkt wspólny ze zbiorem rozwiązań dopuszczalnych w przestrzeni kryterialnej. Długość promienia tego okręgu wyznacza poszukiwana minimalna odległość punktu Y* od rozpatrywanego zbioru. Ilustruje to rys. 4.13.

Punkt K‘ zbioru rozwiązań dopuszczalnych w przestrzeni kryterialnej jest poszukiwanym rozwiązaniem, położonym najbliżej rozwiązania idealnego.

4.4.6. Metoda interaktywna

Omówiona w tym podrozdziale metoda poszukiwania rozwiązania końcowego metodą interaktywną nawiązuje do przedstawionych w poprzednich podrozdziałach metod: generowania rozwiązań sprawnych za pomocą jednej funkcji kryterium oraz metody satysfakcjonującego poziomu kryteriów. Jest to postępowanie itcracyjne. W i-tej iteracji rozwiązujemy ciąg z.adań jednokryterialnych Z„_r gdzie i jest numerem iteracji, natomiast q oznacza numer funkcji celu w rozpatrywanym zadaniu wielokryterialnym. Warunki ograniczające w zadaniu Z,„ to warunki ograniczające wyjściowego zadania wielokryterialncgo oraz pewne dodatkowe warunki, określone na podstawie sformułowanych przez decydenta w poprzednich iteracjach oczekiwań względem poziomu uwzględnianych w modelu kryteriów.

Zestawiamy otrzymane wartości rozwiązań i na ich podstawie tworzymy dwa wektory: wektor ocen akceptowanych oraz wektor ocen optymistycznych. Może się zdarzyć, że wektory te są sobie równe: wtedy kończymy postępowanie, przyjmując otrzymane rozwiązanie jako końcowe. Jeżeli tak nie jest, to korzystając z tych wektorów, decydent określa, czy zamierza kontynuować postępowanie, czy też dokona wyboru rozwiązania końcowego spośród tych rozwiązań zadania Z_iq, którymi aktualnie dysponuje. W przypadku wyrażenia przez decydenta chęci kontynuowania postępowania dokonuje on wyboru kryterium (lub kryteriów)

1    określa minimalną wartość (wybraną z przedziału, którego końcami są aktualne wartości: akceptowana i optymistyczna). Przechodząc do i + 1 iteracji, uwzględniamy te minimalne wartości przy konstruowaniu nowego zbioru warunków ograniczających.

Przykład 4.10^!’

Stosując metodę interaktywną, rozwiążemy zadanie sformułowane w przykładzie 4.2.

' Przykład ten możemy rozwiązać za pomocą programu INTERAKT.KXE.