239

476 Rozwiązania i odpowiedzi

13.27. x*-\, JC^O; y' = R.13.8); tabelka:

t

,xHx+l) .

; asymptoty: y= 1, x = -1, *=0 (ry_s

-lx²-2x x⁴(x+l)² '

X	— CO			-1		2 ^_ 3		0			+ CO
/	0	-	0	— CO	-	0	+	+ 00	— 00	-	0
y	i	\	0	+ 00		27 e ^4m	/	+ oo	+ co	\	1

2x

X² - 1    —

/= 0, gdy ,v=0, /' =

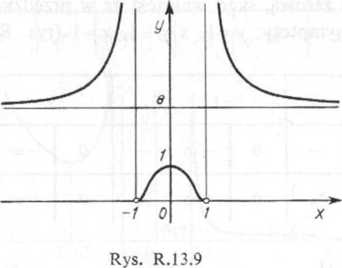
13.28. x#-l, x#l: y=e **-';/ = -_²(3x⁴— 1) t+—iy „_Q (x²-l)⁴    ’

(x²-l)²

gdy A'= -olub.v=df, gdzie a=xF-; asymptoty: y=e, jt= — i,

v 3

jc=1; oś Oy jest osią symetrii krzywej (rys. R. 13.9); tabelka:

X	— CO			-1		—a		0		a		i			+ CD
y"	0	+	+ cc	0	+	0	-	-	-	0	+	0	+ 00	+	0
y'	0	_i_	+ 00	0	+	+	+	0	-	-	-	0	— 00	-	0
y	e	/	+ 00	0	/	f(~a) P		1 M	\	/(«) p	\	0	+ co	\	e

13.29.    Funkcja jest określona dla wszystkich x; przy x = 0 mamy y_m,_x=l; punkty przegięcia ($j2,e~¹¹²), (-£ J2, e~^l‘²) ; asyinptota y = 0.

13.30.    Funkcja jest określona dla wszystkich x; przy x = 4 mamy y_mtx = e²; punkty przegięcia (4 + ^2, e^3/2), (4-^/2, e^3/2); asymptota y=0.

13.31.    Funkcja jest określona dla wszystkich x; przy x=_s/2 mamy y_mxx = j2e''''* a przy x=-j2. mamy y_mi„= -j2e~^lU; punkty przegięcia: (0,0), (±y/6, ±_N/6e^_3/2)l asymptota y-0; miejsce zerowe funkcji x=0.

13.32.    Funkcja jest określona dla wszystkich x#0; przy x = \ mamy y_min = te²; asymptota x = 0; lim >>=+oo, lim y = 0.

*-♦ + 0    x~* —o

13.33.    Funkcja jest określona dla wszystkich x; przy x-\ mamy y_max = f^e^-3; punkty przegięcia mają odcięte: x = 0, x = it.3±_N/3); asymptota y = 0.

13.34.    Funkcja jest określona dla wszystkich x; punkty przegięcia ( — 3a, 10ae~³), (-a, 2ae~²); asymptota y = 0.

13.35.    Funkcja jest określona dla wszystkich x; przy x = 0 mamy _y_min=0 (ostrze).

13.36.    x^($+ k)n (k=±l, ±2,...), okres n; y' =—— ^e‘^8X'    ¹*^m / = lim (1 +

COS X x-*-^rr+0    x-*-$rc + 0

+ tg² x) e'^s* = 0 (por. zad. 12.65), a więc krzywa zbliża się do punktu    0) z prawej

l+sin2A:    .    .

strony stycznie do osi Ox; y =-_z—e^g , w punkcie x = —{n me ma przegięcia,

cos x

gdyż y" nie zmienia znaku (rys. R.13.10); tabelka (w przedziale <—j-it, 4-it)):

X					-ilt		in
y"	+	4-co	0	+	0	4*	4-oo	0	+
y'	+	4- co	0	-1-	+	+	4- oo	0	4"
y	/	+ co	0	/	/ •	/	4-co	0	/

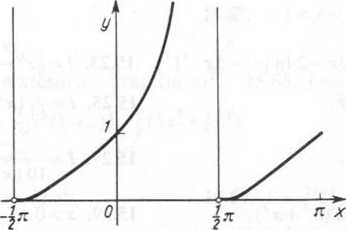
Rys. R.13.10

13.37.    Funkcja jest określona dla wszystkich x; punkt przegięcia (£, 1,59); asymptoty >=0,21 (przy x-+ — oo) i j> = 4,81 (przy x-* + co).

13.38.    Funkcja jest określona dla 0<.x^l; punkt przegięcia (^(5 — ^5)*0,28, 1,74)

13.39.    Funkcja jest określona dla .v>0; asymptoty y=l,57, y= — \,51 (przy