250(1)

in, pierwiastkiem pojedynczym równania charakterystycznego. Wobec tego całką szczególną danego równania będzie

y\ — AxⁱĄ-x{Bx^l-\-Cx^JrD)e~^x

Podstawienie tej funkcji do danego równania niejednorodnego prowadzi do równości

2A+ [3Bx²-H2C-12B);c-t- ((>B-AC+D)\e7^x = 1 - 6x²e~^x z której otrzymujemy układ równań

2A = 1, 3B = -6, 2C-125 = 0, 6B-4C+D = 0

1

po rozwiązaniu którego znajdujemy A = —, B = —2, C = —12, D = = —36. Zatem

y_x = y x²-2x(x²+6x+\8)e-^x

y = u-\-y\ — C\-\-CiX-\-C^e *-j- — x~ — 2.vęjc²6at-f- 18)e

1122. Na podstawie ogólnego wzoru (*) znaleźć całki szczególne równań

1)    y"-\-4y' -\-Ąy = e^_2*sec²A-

2) /'+5/+6>.= (^+ir-

3) /"-3/'+3/-^ = 5x³e^x+3e^2x

4)    y"-\-4y = cos³*

Rozwiązanie: 1) Piszemy najpierw równanie charakterystyczne r¹ -i 4r+4 — 0 i znajdujemy, jego pierwiastki r, = - 2, r₂ = —2. Podstawiając następnie te pierwiastki oraz funkcję q(x), występującą po prawej stronie danego równania, do wzoru (2) i całkując dwukrotnie, otrzymamy szukaną całkę szczególną

p, = e~^2x I (/sec²**/*) dx = e^-2* j tg-xdx — —e~^2xln cos*j

2) Pierwiastkami równania charakterystycznego r²+5r+6 = 0 są r₍ = =—3, r₂ = 2. Podstaw iając je wraz z funkcją występującą po prawej stronie danego równania do wzoru (2), otrzymamy

y_l — e~^lx J & [ j'e^2r(e^2:c-rl) ² d*] dx

Osobno obliczamy całki

/, = | e²T(e²x-j-l)^_ 3 dx = ~ j (e²x-rl) ³ r/(e²x+l) — —(e²x-f-l) ²

h = f e*h dx - - f —    = —ln [e^xĄ- l'e^2x+l)

J    J }/(c^x)²+l

Wobec tego szukaną całką szczególną danego równania będzie jj = —e^_3xln (e^x-|- j e^2x-j-l)

3) Równanie charakterystyczne r³—3r²+3r—1 =0 ma pierwiastki r_i — r₂—r₃=l. Podstawiając te pierwiastki oraz funkcję występującą po prawej stronie danego równania do wzoru (3) i całkując trzykrotnie,

otrzymamy

)’i = e* | {J [j (5.v³+3e^x) dĄ dx| dx =

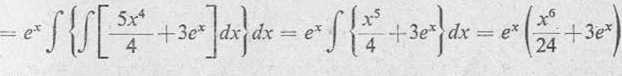
4) Pierwiastkami równania charakterystycznego r²4-4 = 0 są r_u2 = \ = ±2/. Na podstawie wzoru (2), mamy

y i

= e^2ixJ

^4ix i I e^2,xcos³

xdxjdx

Wyrażając cos³* przez funkcje wykładnicze (wg wzoru Eulera, rozdz. IX, § 6) i całkując, znajdujemy

/] = j e^2,xeos³xdx — j' e^2ix(e'^x -J-e~‘^x)¹dx —

/ e^5ix	„3ix 1 ^L	3e^ix	e-ix'
\ 5/	^1 i '	^1 i	i i

e ^sixj <7* =

= -g I (e^iix-\-2c^2,x-\-3e^ixĄ-e~^,x)dx —

\-e~^ix+3e-^3ix-

4*

^1 1	/ gix e IX	e-3ii ^		c-^5U\
8/ ^1	1 5/ /	i		5/ /
		L	I e^Mx	^i.v
	C i 2	8 i^2	5

503