Image53 (12)

104

Wobec tego możemy napisać różniczkowe równanie ruchu kulki w następującej postaci

104

d²x

dt²

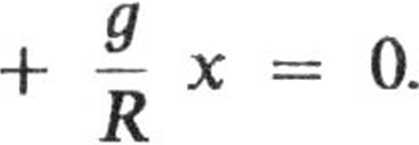
Stosując standardowe podstawienie co² kowe drugiego rzędu, liniowe jednorodne

9

R

dostajemy równanie różnicz-

d²x

dt²

4- co²x = 0.

Całka ogólna tego równania jest postaci (patrz rozwiązanie zad.2.9)

- icat

C, e^iCit + C

Stałe C₁ i C₂ wyznaczamy z warunków początkowych:

t

0,

x(0)

R,

x(0) = 0,

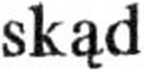
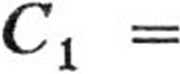
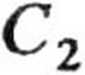
R

2 ’

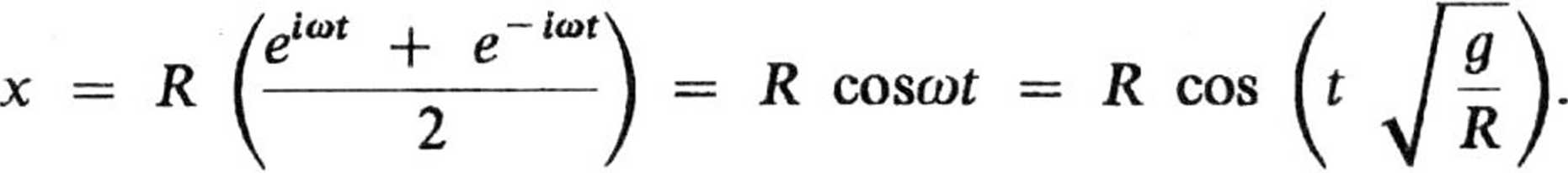
Czas, w ciągu którego kulka osiągnie środek Ziemi, obliczamy z równości

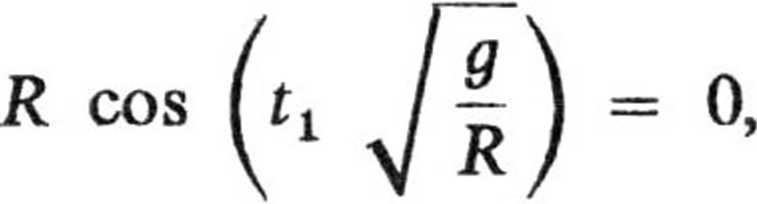
skąd

Prędkość kulki obliczamy ze wzoru

v =

dx

dt

= — R

R

sin t

9

R

Kulka minie środek Ziemi z prędkością

v

= R

9

R

sin t

9

R

= 7,9 [km/s]

ę

2.47. Żądanie zawarte w zadaniu zostanie spełnione wtedy, gdy maksymalne przyspieszenie ruchu drgającego deski będzie równe co najwyżej przyspieszeniu ziemskiemu spadku swobodnego. Wychylenie deski z położenia równowagi jest opisane równaniem

x = x_a cos (Dt,

a więc przyspieszenie deski

x = —x_Qw² cos (Dt = — co² x.

W ruchu drgającym przyspieszenie osiąga wartość maksymalną w punktach maksymalnego wychylenia. Zatem warunek zadania będzie spełniony dla takiej wartości cu, dla której

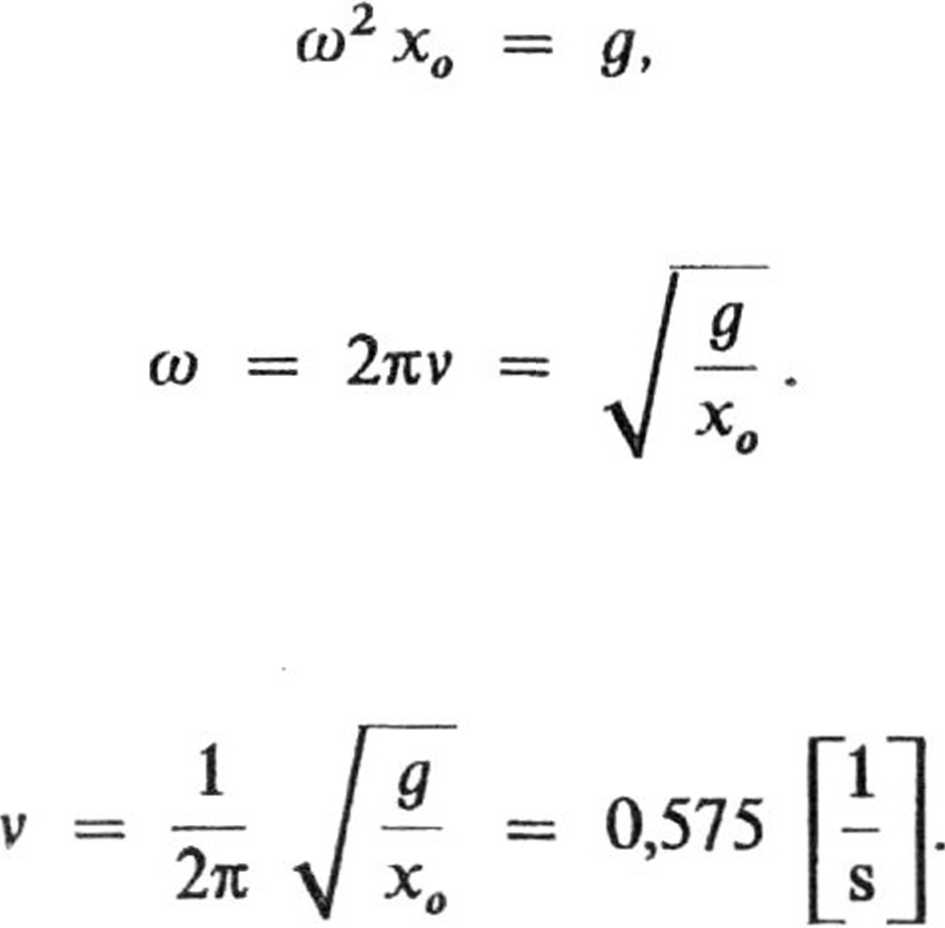
czyli dla

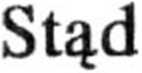
2.48. W przypadku granicznym warunek dla sił przybiera postać

2n

m x

T

fung,