Image34 (19)

66

stąd

66

C, =

2

x₀ + i v₀

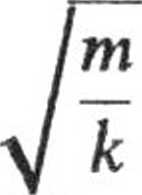
C

— IV.

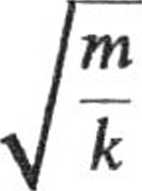
2

Wobec tego rozwiązanie szczególne równania różniczkowego jest wyrażone wzorem:

z(t) =

2

⁰ ' e^^mt + e J^mt

4- i

v

O

m

k

2

x₀ cos/i

k

m

Zatem rozważane ciało porusza się po hiperboli o równaniu parametrycznym

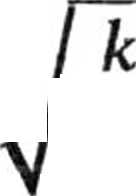
x(t) = x₀ cos/i / — t,

m

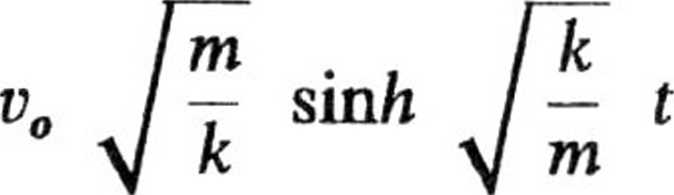
y(t) =

dla t ^ 0, które - po wyeliminowaniu czasu - można zapisać w postaci ogólnej

y

v

m

k

1

Dla k < 0 równanie charakterystyczne ma dwa rozwiązania zespolone

^ri =    ¹

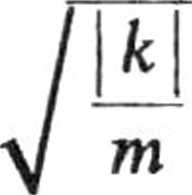
r-, = —i

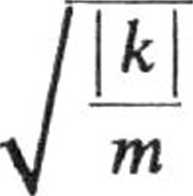
Otrzymujemy zatem rozwiązanie ogólne postaci

¹ V m *

m

z(t) = C.    + C

(C_A + C₂) cos

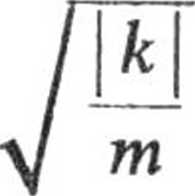
t + i (C_i — C₂) sin

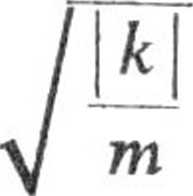
t.

Z warunków początkowych wynika, że

m

k

Cl =

— v.

m

k

skąd otrzymujemy rozwiązanie szczególne równania różniczkowego

z(t) — x_Q cos

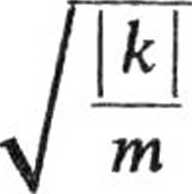
t + i V.

m

k

sm

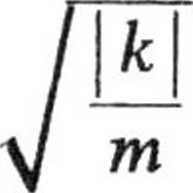
t.

Jest to równanie elipsy, które możemy zapisać w postaci parametrycznej

<

x(t) =

x_a cos

m

k

y(t) =

V.

m

k

t,

sin

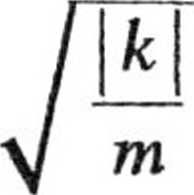
t

dla t

0, bądź w postaci ogólnej

-f

y

V

O

m

k

= 1

Sprawdzając warunek

rot F = 0,

łatwo wykazać, że rozpatrywane pole jest zachowawcze.