3 5 2

Piotr Bieranowski - ćwiczenia z WYTRZYMAŁOŚCI MATERIAŁÓW, CZ. III    2015/16

Odp. : Płyta obróci się o pewien kąt (p dokoła stałego przegubu. Punkt C płyty będzie się poruszał po normalnej do promienia AC, zajmie więc położenie C, (rys. 3 b). Pręt 2 musi się wydłużyć od Al₂ i obrócić tak, aby dolny koniec C pręta 2 znalazł się w punkcie C, (na rys. 3b punkt C przemieszcza się wzdłuż osi pręta o odcinek AU, a następnie w kierunku prostopadłym od osi pręta - do punku C,).

Obydwa pręty wydłużą się, a więc działają w nich siły rozciągające (rys. 3 c).

Z równań równowagi wykorzystamy tylko równanie momentów

i

ZM ,= M_{) — -S, -3a-S-, • 4a = 0

Brakujące równanie otrzymamy z porównania odkształceń (rys. 3 b).

Ponieważ AB = 3a i AC = 5a, po oznaczeniu odcinka CC, = x, możemy napisać

x = — AL

AL x tg<p = —^L = — 3 a    5a

Kąt C_XCD (rys. b) wynosi a, a więc cosa = Al₂/x, zaś z trójkąta ADC znajdujemy

5    3

cosor = 4/5, zatem x = —Al₂. Z porównania otrzymanych wyników mamy Al_} = — Al₂, a po

zastosowaniu prawa Hooke'a otrzymujemy brakujące równanie

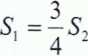
Z powyższych równań otrzymujemy

5, =—^± = — ³°⁰⁰°[^N •^m] ₌ 6000[N] = 6[kN] 25 a 25 l[m]

. ₌±K>

²    25 a

4 50000[N-m] 25 l[m]

= 8000[N] = 8[kN].

Zadanie 4. Zaprojektować stalową sprężynę śrubową, która pod działaniem siły P = 500[N] wydłuży się o /l = 6[cm]. Naprężenie dopuszczalne na skręcanie stali sprężynowej k_s = 400[Mpa], G = 8,5 ■ 10⁴[Mpa], a stosunek średnic Dld = 10.

Odp. : Ze wzoru

*^PD

T =-< K

" rr»ov    - “i ' ^ c

str. 5