328 329

328

7.2.2. Właściwa numeracja zdarzeń

Dla oznaczenia poszczególnych czynności wchodzących w skład sieci można oprócz dotychczas wprowadzonych oznaczeń używać symboli (;', J), gdzie i oznacza numer zdarzenia początkowego, a j — numer zdarzenia końcowego. Numeracja zdarzeń jest właściwa, jeżeli numer wierzchołka stanowiącego początek dowolnego występującego w sieci łuku jest mniejszy od numeru wierzchołka kończącego ten łuk. Jeżeli zatem sieć składa się z n wierzchołków, to właściwa ich numeracja zapewnia, że początek sieci odpowiadający rozpoczęciu przedsięwzięcia ma numer 1, a koniec sieci odpowiadający zakończeniu przedsięwzięcia ma numer n.

Wykorzystując przedstawioną powyżej metodę, ponumerujemy zdarzenia w sieci przedsięwzięcia opisanego w przykładzie 7.1.

Jedynym zdarzeniem początkowym w rozpatrywanej przez nas sieci jest zdarzenie a, więc nadajemy mu numer 1. Następnie usuwamy to zdarzenie oraz wszystkie rozpoczynające się w nim czynności. Otrzymany w ten sposób graf przedstawiono na rys. 7.2.

Rysunek 7.2

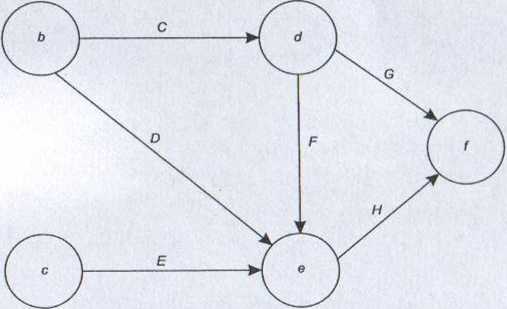
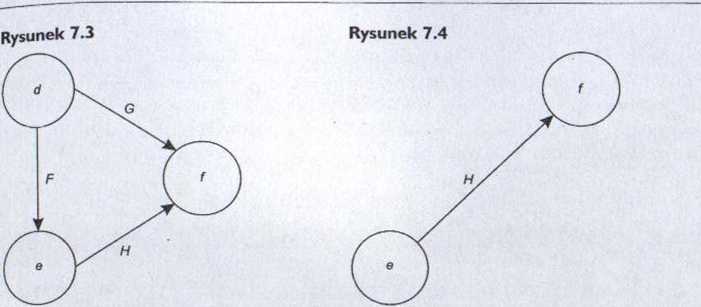
Otrzymaliśmy graf o dwóch zdarzeniach początkowych: b i c. Zdarzeniom tym nadajemy kolejne numery, 2 i 3, oraz usuwamy je z grafu, podobnie jak wszystkie czynności rozpoczynające się w tych zdarzeniach (rys. 7.3).

Kontynuując to postępowanie, nadajemy zdarzeniu d numer 4 i usuwamy je z grafu (rys. 7.4). Z kolei zdarzeniu e nadajemy numer 5, a zdarzeniu końcowemu/— numer 6.

Warto zauważyć, żc właściwa numeracja zdarzeń nie jest określona w sposób jednoznaczny, wierzchołkom b oraz c mogliśmy bowiem przyporządkować numery 3 i 2 (a nie 2 i 3 jak poprzednio).

W rozpatrywanej przez nas sieci mamy (tablica 7.2):

Tablica 7.2

Czynność	Numer zdarzenia stanowiącego początek czynności	Numer zdarzenia kończącego czynność
A	1	2
B	1	3
C	2	4
D	2	5
E	3	5
F	4	5
G	4	6
H	5	6

Można łatwo sprawdzić, że w zaproponowanej numeracji numer zdarzenia stanowiącego początek dowolnej czynności jest mniejszy od numeru wierzchołka kończącego tę czynność, czyli spełniony jest warunek właściwej numeracji zdarzeń.

7.3. Metoda ścieżki krytyczne]

Rozpatrzymy sytuację, w której realizację każdej czynności opisuje jeden parametr charakteryzujący czas trwania tej czynności.

Możemy sformułować następujące pytania:

1. Jaki jest najkrótszy czas, w którym można zakończyć realizację projektu (czyli najkrótszy czas realizacji projektu)?