4520

Szósty tydzień - przykłady

l-

1-1 l-l] I 1 —1 l]

f-l] f I • 0 + (-1) ■ (-1) + 1 • 2 + (—1) ' ( 3) | | 2    (M)0+l.(-l) + (-l)-2+l.(-3)J

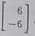
Zatem rozwiązaniem układa równań jest para tuadersy

• Przykład 6.3

a) Rozwiązać równanie macierzowe 3

_ _v. ([-H*[-::]

b) Rozwiązać układ równań macierzowych

[ x+y =	1 1 0 1
^1 2X + W =	1 0 0 1

• Przykład 6.4

Obliczyć kilka początkowych potęg macierzy A, następnie wysunąć hipotezę O postaci macierzy Aⁿ, n € jV, i udowodnić ją za pomocą indukcji matematycznej.

i o ijH

a) A

= [ó I

; b) A =

0    1 o

1    0 1

Rozwieranie

Dodawanie i odejmowanie maderzy oraz mnożenie macierzy przez liczbę mają te tamę własaofd jak zwykle działania w zbiorze liczb rzeczywistych. W obu przykładach wyko-njztaay te własaoócL

a) Mamy    » - •

Rozwiązanie n) Mamy

■r"

i

= .l[ II

2 [ —2i 4j

2X =

<=> X =

«=> X

Rozwiązaniem równania jest macierz X =

U

BB

I

i

o -

‘] “ [*o t-o“] = [~ó -?].

■

A'-AA

A* 11 • A³ |

A* a A² ■ A? «

|| ■ A^a • A³ §

Na podstawie zauważonych prawidłowości w macierzy A* d|* hipotezę o postaci tej macierzy

-1 0 0 -1

-J 0 0 -1

-1 0 0 -1

-i -1

0 i

-i -I 0 i

• 1 0 -i

*jŁ.

^Rs=1.2.3.4_l5

^wJwwamy

b) Odejmując od drogiego równania podwojone pierwsze otrzymamy

sir.

Odejmując teraz od drugiego równania potrojone pierwsze uzyskamy

■■Slllliil

i 1

0    -i

-1 0 0 -1

-i -1 0 i

1    0 0 1

dla n = 4ł + 1, dla n=4* + 2, dla n=4k + 3, dla

n=4ł + 4,

gdzie k