4521

63

Macierze i wyznaczniki

Szósty tydzień - przykłady

69

Prwpronadiimy teraz dowód l«?J hipotezy dla n * 4i + 1 za pomoc* indukęji inatcma-lycinej. Udowodnimy więc wzór

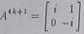
Zatem z prawdziwości hipotezy dla liczby naturalnej n wynika, jej prawdziwość dla liczby n+1. Ponieważ hipoteza jest prawdziwa dla n = 1, więc z zasady indukcji matematycznej wynika, że jest ona prawdziwa dla każdej liczby naturalnej.

dla k 3 0.1.2.....Dla * = 0 i * = I wzór jest prawdziwy. Niech k będzie dowolną liczb*

naturalną. Załóżmy, że wzór jest prawdziwy dla k. Pokażemy, że jest on prawdziwy takie dla k +1. Mamy

• Przykład 6.5

Układając odpowiednie układy równań znaleźć wszystkie macierze zespolone X spełniające podane równania macierzowe:

induityiftf

■HU

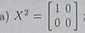
Rozwiązanie a) Niech X w

b) X

1 121	112'
[oi lj“	3 5 8

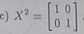
Zatem z prawdiiwośd hipotezy dla k wynika jego prawdziwość dla A + 1. Ponadto wzór jat prawdziwy dla * a I, więc z zasady induktyi matematycznej wynika, ie jest on prawdziwy dla kaidej liczby naturalnej oraz dla ł«0.

Uwaga*. Wzór ogólny na ntą potęgę macierzy A ma postać

A*

• P»*i)

. nu i

^wnT

(-0" J

a b c d

Równanie X³ =

, gdzie a, b,c,d € C, będzie szukaną macierz*. Wtedy

X⁷ =

a 6		a b
c d		c d

? + bc ah + hdl c + cd bc + d³ J

1 0 0 0

jest zatem równoważne układowi równań

a⁷ +bc = 1, 6(a + d) ■ 0,

c(a + d) = 0, bc + d⁷ = 0.

gdzie £(■) oznacza część całkowi* liczby u. b) Mamy

Al*A =	r i o 0 10 [l 0 1
A^3 o A - A =	■| 0 1 0 1 0 1 o 1
A^9 = A • A^3 m	J 0 1 0 1 0 1 0 1J
A' = A^3A^3 =	2 0 2 0 1 0

U 0 2fi

Na podstawie obserwacji macierzy A* dla n =

1.2.3

4 wysuwamy hipotezę, że

Z drugiego równania wynika alternatywa warunków 6 = 0 lub a +d a 0. Rozważmy zatem pierwszą możliwość 6 = 0. Wtedy pierwsze równanie przyjmuje postać a⁷ =1, a czwarte d³ => 0. Stąd a = 1 lub u = -1 oraz d = 0. Ponieważ a - d = ± 1 = 0. więc z trzeciego równania wynika, ic c = 0. Ostatecznie otrzymaliśmy w tym przypadku dwa rozwiązania a s I, 6 b 0, c = 0, d = 0 lub a = — 1, 6 = 0, c = 0, i — 0. Jeżeli natomiast a + d = 0, to drugie i trzecie równania s* spełnione dla dowolnych liczb zespolonych hic. Równanie czwarte przyjmuje wtedy postać 6c + «^ł = 0 i jest sprzeczne z pierwszym równaniem. Uzyskana sprzeczność wyklucza tę możliwość. Rozważane równanie macierzowe ma zatem tylko dwa rozwiązania

X =

1 0

o o

oraz

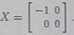
b) Z postaci równania wynika, że macierz .Y jest macierz* kwadratów* stopnia 2. Niech zatem X = “ ^ , gdzie a, b, c, d € C Równanie macierzowe przyjmie wtedy postać

Aⁿ =

2"“^ł

0

Oii-l

0    ar” i

1    o

0 2"’* J

Przeprowadzimy dowód tej hipotezy za pomoc* indukcji matematycznej. Dla n =*1 hipoteza ta jest prawdziwa. Niech teraz n będzie dowolną liczb* naturalną. Załóżmy, hipoteza jest prawdziwa dla liczby n. Pokażemy, że jest ona prawdziwa dla liczby n +1. Mamy

uImhIi	r2*-l o 2—^1 1	i o r	fn	0 2°
A ~	0 1 0 •	0 10.	= o	1 0
Iftilufccjrjflt	[2U-I 02->J	1 0 lj	U"	0 2"

a a + b 2a *|* b c c + d 2e + d

która jest równoważna układowi równań

I 1 2 3 5 8 '

« = 1.

a + 6 = 1,

2a + b = 2, c = 3. c -I- d = 5, 2c + ż ■ 8.

i"*»