3tom209

6. GOSPODARKA ELEKTROENERGETYCZNA 420

poprzednio ze wzoru

(6.85)

gdzie E, — średnia zdyskontowana, jednakowa we wszystkich latach, roczna produkcja energii elektrycznej, kW • h/a.

6.3.3. Wybór rozwiązania optymalnego

Całkowite koszty roczne, określone z uwzględnieniem rozkładu czasowego nakładów, stanowią podstawę wyboru rozwiązania optymalnego zgodnie z zasadą optymalności (6.74). Najczęściej spotykanym zagadnieniem w zakresie tak pojętej optymalizacji w elektroenergetyce jest porównanie dwóch wariantów rozwiązania technicznego o charakterze inwestycyjnym lub eksploatacyjnym, w których koszty roczne są różne, efekty natomiast —jednakowe. Warunkiem porównywalności wariantów jest wówczas równość efektów.

Jeżeli w dwóch porównywanych ze sobą wariantach A i B efekty równoważne są jednakowe, E_rA = E_rB, to można dla każdego wariantu określić: zdyskontowane nakłady inwestycyjne K_ndA i ze wzoru (6.80), współczynniki rozszerzonej reprodukcji r . i r_B ze wzoru (6.63), równoważne koszty eksploatacyjne K„_A i K_rrB ze wzoru (6.82) i stąd całkowite koszty roczne K_rA i K_rB ze wzoru (6.84).

Najczęściej spotyka się przypadek nierówności nakładów, a więc w wariancie, w którym nakłady inwestycyjne są większe, np. K„_dĄ > K^n, występują mniejsze koszty eksploatacyjne K_erA < K„_B. Optymalnym jest wówczas wariant, w którym całkowite koszty roczne są niższe. Jeśli zatem K_rA < K,_a. to wariant A przyjmuje się jako optymalny. Powyższy sposób rozumowania przedstawiono poglądowo w tabl. 6.7.

Tablica 6.7. Schemat wyboru wariantu optymalnego spośród dwóch rozwiązań o jednakowych lub niejednakowych efektach

Warianty porównywane	Efekty jednakowe		Efekty niejednakowe
	A	B	A	B
Efekty roczne Nakłady inwestycyjne Koszty rozszerzonej reprodukcji Koszty eksploatacyjne Całkowite koszty roczne	= Er. > K«, Kr* > Err* < K„a K* < K.		E,a + AE,= F.,a > Kt,. KrrA * ó > K„b K„a~AK„<K„, K,,+A K>K„
Jednostkowe koszty roczne	Ka ^<		k -JSl±>k ^KrA ~ r- ^>K'B ~ r-
Wariant optymalny	A		—	B

Jeżeli natomiast efekty równoważne w obu porównywanych ze sobą wariantach A i B nie są jednakowe, np. E_rA < E_rB, to należy w wariancie o mniejszym efekcie dodać do efektu E_rA efekt uzupełniający AE„ tak aby doprowadzić do zrównania efektów, czyli do spełnienia podstawowego warunku porównywalności wariantów. Dopiero wówczas można obliczać koszty roczne, przy czym do kosztu rocznego K_rA należy w tym przypadku dodać koszt roczny A K, niezbędny do uzyskania efektu uzupełniającego. Optymalnym jest ten wariant, w którym całkowite koszty roczne z uwzględnieniem dodatkowego kosztu rocznego AK, są niższe.

Taki sposób rozumowania, prowadzący do wyboru wariantu optymalnego przy różnych efektach produkcyjnych, przedstawiono również w tabl. 6.7.

Uproszczony sposób postępowania ma miejsce przy wyborze wariantu optymalnego spośród rozwiązań charakteryzujących się niejednakowymi efektami produkcyjnymi wówczas, gdy różnice między efektami E_rA i £,_g są niewielkie. Polega on na tym, że

—    zamiast kryterium minimalizacji całkowitych kosztów rocznych (6.74) z uwzględnieniem efektów i kosztów uzupełniających — można stosować kryterium minimalizacji jednostkowych kosztów rocznych (6.75). Optymalnym jest ten wariant, w którym jednostkowe koszty energii k, są niższe (patrz tabl. 6.7).

Podobnie postępuje się przy większej liczbie wariantów, spośród których jako optymalny wybiera się ten w^rariant, w którym całkowite koszty roczne z uwzględnieniem ewentualnych kosztów dodatkowych, niezbędnych do uzyskania efektów uzupełniających, są najniższe.

W sposób uproszczony można także określać jednostkowe koszty roczne i poszukiwać wariantu o najniższych jednostkowych kosztach energii.

Szczególnym przypadkiem zadania optymalizacyjnego jest wybór wariantu optymalnego spośród nieskończonej liczby możliwych rozwiązań technicznych. Występuje on wówczas, gdy zależność kosztów rocznych K, od w^rybranej wielkości zmiennej x da się przedstawić w postaci funkcji analitycznej K_r = f(x). Optymalizacja polega wtedy na następujących czynnościach:

—    znalezieniu ekstremum tej funkcji przez przyrównanie pierwszej pochodnej do zera

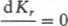
dx

(6.86)

—    zbadaniu znaku drugiej pochodnej dla potwierdzenia, że znalezione uprzednio ekstremum stanowi rzeczywiście minimum funkcji K_r = f(x);

—    obliczeniu wielkości zwanej też wielkością ekonomiczną lub gospodarczą, przez rozwiązanie równania wynikającego ze wzoru (6.86).

Przykładem takiej optymalizacji jest poszukiwanie ekonomicznej gęstości prądu w linii elektroenergetycznej, tj. takiej gęstości, przy której całkowite koszty roczne przesyłu energii elektrycznej tą linią są najmniejsze.

Z warunku (6.86) otrzymuje się następujący wzór na optymalną (ekonomiczną) gęstość prądu, wyrażoną w A/mm²:

(6.87)

w którym: c — składowa jednostkowego kosztu budowy linii zależna od przekroju przewodów, zł/(km ■ mm²); y — konduktywność materiału przewodowego, m/(fi • mm²); r — współczynnik rozszerzonej reprodukcji, określony wzorem (6.63); r_a — współczynnik rocznych stałych kosztów eksploatacyjnych, określony wzorem (6.65); 5_S — współczynnik udziału w szczycie systemu, określony wzorem (6.69); k_P —jednostkowy roczny koszt strat mocy, zł/(kW • a); 9 — stopień strat obciążeniowych, określony wzorem (6.48); T = 8760 h/a — okres roku; k_E ■— jednostkowy koszt strat energii, zł/(kW • h).

Ze wzoru (6.87) wynika, że ekonomiczna gęstość prądu jest większa, jeżeli:

—    stosuje się droższy materiał przewodowy zamiast tańszego;

—    stosuje się materiał przewodowy o większej konduktywności, np. miedź zamiast aluminium;

—    koszty jednostkowe strat mocy k_P i energii elektrycznej k_E są niższe;

—    stopień strat obciążeniowych 9 jest mniejszy, co wiąże się z mniejszym stopniem obciążenia m, czyli mniejszym czasem wykorzystania mocy szczytowej T_s.