85

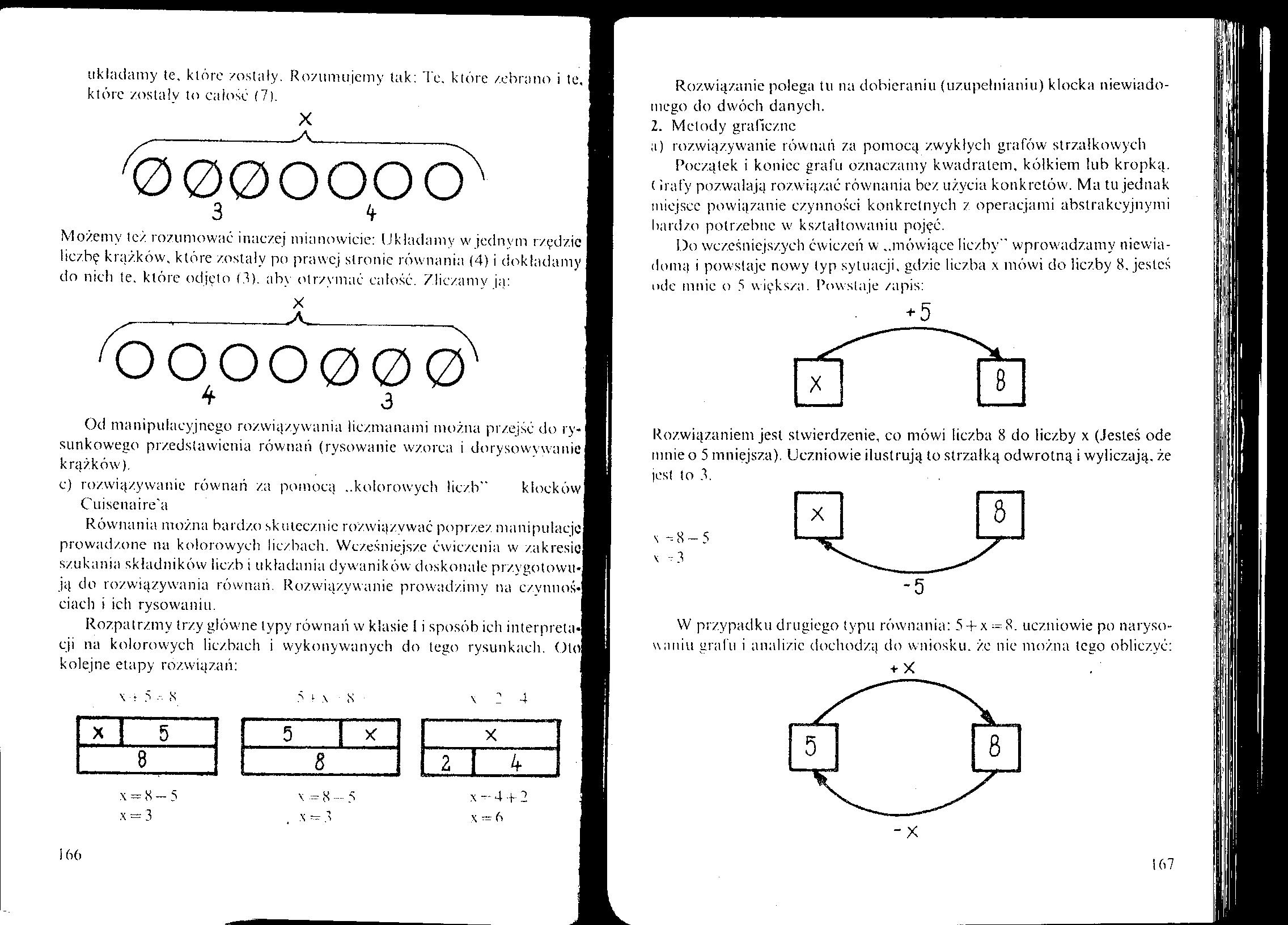
układamy te, które /ostały. Rozumujemy tak: Te. które zebrano i te, które zostały to całość (7).

X

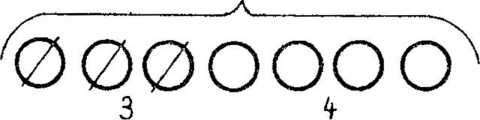
Możemy też rozumować inaczej mianowicie: Układamy w jednym rzędzie liczbę krążków, które zostały po prawej stronic równania (4) i dokładamy do nich te, które odjęto <Ó). aby otrzymać całość. Zliczamy ją:

X

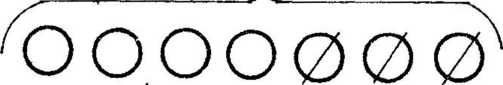
4    3

Od manipulacyjnego rozwiązywania iiczmanami można przejść do rysunkowego przedstawienia równań (rysowanie wzorca i dorysowywanie krążków).

c) rozwiązywanie równań za pomocą ..kolorowych liczb’* klocków Cuisenaire'a

Równania można bardzo skutecznie rozwiązywać poprzez, manipulacjo prowadzone na kolorowych liczbach. Wcześniejsze ćwiczenia w zakresie szukania składników liczb i układania dywaników doskonale przygotowują do rozwiązywania równań. Rozwiązywanie prowadzimy na czynnościach i ich rysowaniu.

Rozpatrzmy trzy główne typy równań w klasie I i sposób ich interpretacji na kolorowych liczbach i wykonywanych do tego rysunkach. Oto kolejne etapy rozwiązań:

x1    5    5

8 8

X

x -- 4 f 2 x — 6

Rozwiązanie polega tu na dobieraniu (uzupełnianiu) klocka niewiadomego do dwóch danych.

2. Metody gra liczne

a) rozwiązywanie równań za pomocą zwykłych grafów strzałkowych Początek i koniec grafu oznaczamy kwadratem, kółkiem łub kropką. (i rafy pozwalają rozwiązać równania bez użycia konkretów. Ma tu jednak miejsce powiązanie czynności konkretnych z operacjami abstrakcyjnymi ha rdzo potrzebne w kształtowaniu pojęć.

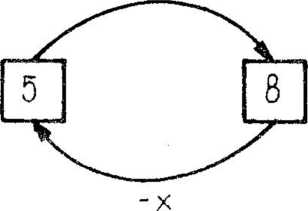
Do wcześniejszych ćwiczeń w ..mówiące liczby" wprowadzamy niewiadomą i powstaje nowy typ sytuacji, gdzie liczba x mówi do liczby 8, jesteś ode mnie o 5 większa. Powstaje zapis:

+ 5

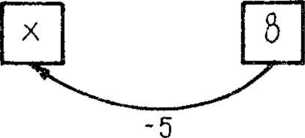
Rozwiązaniem jest stwierdzenie, co mówi liczba 8 do liczby x (Jesteś ode mnie o 5 mniejsza). Uczniowie ilustrują to strzałką odwrotną i wyliczają, że jest to y.

W przypadku drugiego typu równania: 5 +x =8. uczniowie po narysowaniu grafu i analizie dochodzą do wniosku, że nie można tego obliczyć:

+ X

67