Capture114

Przy badaniu istotności równicy między dwiema wariancjami p_rA|ln, hipotc/ę zerową //,. rrf = <TŚ = rr Następnie znajdujemy stosunek dwi*h ^: cią/onyeh oszacowań wariancji. Są to:

*»    * A^r, - I

ora/

, UX-X_Z)'

Afj-1

Nie ma żadnych podstaw. by / góry decydować, które os/acowanic v._anjr. powinno się umieścić w liczniku, a które w mianowniku stosunku / W p_r^ * cc większe / dwóch oszacowań wariancji umieszcza się zawsze w liczniku ₄ mniejsze w mianow niku. W efekcie stosunek F jest zawsze większy <_H| icdrniśc, Stosunek F obliczamy, porównujemy z tablicą F w Dodatku i określamy po_/10m

istotności.

Km

W tym miejscu pojawia się niewielka komplikacja. Otóż otrzymany po/jn-j istotności należy podwoić Tablica F pokazuje wartości wymagane dla istotności

na poziomie 5 i 1 procent Przy porównywaniu wariancji w dwóch grupach nie/* Icżnych stają się one poziomami 10 i 2 procent. Przyczyna tej komplikacji lc/y * fakcie, źc większa / dwóch wariancji została umieszczona w liczniku stosunku F Znaczy to, że uwzględniliśmy tylko jedną połowę rozkładu / Musimy nie ty Il u uwzględnić prawdopodobieństwo uzyskania al/rj. lecz także prawdopodobieństw uzyskania .v;/s'|. Gdy interesujemy się istotnością różnicy niezależnie od kierunku, wymagany procent poziomów prawdopodobieństwa uzyskujemy, po prostu poduj. jając ten. który uwidoczniony jest w tablicy F.

Tablicą F posługujemy się przy przeprowadzaniu analizy wariancji (zob rozdział 15). przy której na szeroką skalę wykorzystuje się stosunek / W anahzrc wariancji decyzję o tym. które oszacowanie wariancji umieścić w liczniku, a które w mianowniku, podejmuje się. biorąc pod uwagę inne kryteria aniżeli ich względni wielkość. Stąd w analizie wariancji stosunek F przybiera czasami wartość mnicjuą od jedności, a w tablicy F /najdują się odpow iednie prawdopodobieństwa, mc wymagające podwajaniu.

Rozważmy przykład W próbie liczącej 31 chłopców i 26 dziewcząt zastosowano pewien test psychologiczny. Suma kwadratów odchyleń I(A’ - W wynosi 1926 dla chłopców i 2875 dla dziewcząt. Nic obciążone oszacowania wariancji otrzymujemy, dzieląc sumę kwadratów przez liczbę stopni swobody Tak więc Jl dla chłopców wynosi 31 — 1= 30. dla dziewcząt zaś 26 - 1 = 25 Oszacowanie wariancji dla chłopców wynosi 1926/30 = 64.20. a dla dziewcząt 2875/25* = 115.00.

Czy chłopcy różnią się w sposób istotny od dziewcząt pod względem zmienności w wynikach tego testu? Stosunek F wynosi 115.00/64.20= 1.79 Liczba df dla liczniku równa jest 25. dla mianownika zaś 30. Porównując otrzymane F i

,2.5. Istotność różnic

między wariancjami skorelowanymi

* przypadku danych obejmujących pary pomiarów dwie wańmcje mc , gikami niezależnym. Dane lak.e otrzymujemy, gdy te v.»mc osobs badanu , j^sch różnych rodzajach warunków eksperymentalnych ais, >,^_U}cm>    ,,

_;jJfmc Na pr/yklad w fcksperymcnc.e badającym wpływ „dd/iaKwm cdukacy _Bych w zmiany* postaw możemy dokonać pomiaru postaw, zastosować oddziały-edukacyjne, a następnie ponownie dokonać pomiaru posuw Mo/cmy i, '_r .jo** hipotezę, że nastąpi pewna zmiana w wariancji wyników testu posuw wanancji może znaczyć, żc podjęte oddziaływania edukacyjne wpłynęły na •tmoctńetue istniejących postaw, wywołując bardziej skrajne postawy wind osób ./.oujących miejsca na obu krańcach kontinuum postaw Zmniejszenie mc warian-natomiast moz.e znaczyć, że Oddziaływania edukacyjne wpłynęły na reęrcsjc w kierunku większej jednolitości.

Jeżeli i Ą są dworna nie obciążonymi oszacowaniami wariancji, u r _!Cst IkcUj-i między parami pomiaróyv. to wielkość

*12.6)

(*f-^)V^T 2

^s]Ą{ I- rj₂)

au nvkl.nl 11 N - 2 stopniami swobody.

Dli przykładu przyjmijmy, żc s\ i a; są me obciążonymi oszacowaniami wj nacji wyników uzyskanych w badaniu skalą postaw przed i po przeprowadzeniu śłii/Jihwań edukacyjnych. Niech .vf = 153,20. as; = 102,51, przy N - 38. Korelacja między pomiarami postaw dokonanymi przed i po zastosowaniu oddziaływań efekacyjnych wynosi 0.60. Czy te dwie wariancje różnią mc między sobą w sp.>sob uwity ’ Przeprowadzamy obliczenia:

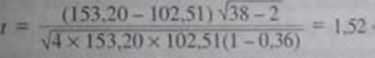
Liczba stopni swobody wynosi 38-2 = 36. Dla istotności na poziomie > procent •ynugana jest wartość t równa lub większa około 2,03. Dane. który mi dysponujmy, są zatem niewystarczające, by odrzucić hipotezę zerową. Nie możemy twter-f< działania edukacyjne wpłynęły na zróżnicowanie postaw