CCF20090601011

10. Wyznaczyć kwadraturę 4-punktową (3. stopnia) Gaussa. Obliczyć za jej pomocą całkę

6/

I

3 -5sin

^f nx^

dx.

\ •+

y

Kwadratura 4-punktowa: I(/) = Aq/(xo) + A\fix\) + A₂f[x₂) + A₃f(x₃). Dla kwadratury Gaussa procedura jest następująca:

a) Obliczamy N + 2 wielomianów ortogonalnych - u nas będzie to 5 wielomianów (od 0-wego do 4-tego),

2/ -1    i-1

bo N = 3. Najłatwiej - wielomiany Legendre'a: Po = 1, P\ -x, P_t = —-—x ■ P_t__x -

P.

7-2

l

=> ^P2 =

2-2-1    2-1    ,    3    ₂    1    _n    2-3-1

-X • A"---1=— X--, P'=-X

2    2 2 2    ³

/

2 2

^A 3-1

5 ₃    3

X = —x —X, 2 2

2-4-1 (5 ,    3 ^ 4 — 1^3 ₂ O

— x“--

— X v2

35 ₄    15 ₂    3

= —x--x“ + —

8    4    8

b) Kwadratura 4-punktow^;a Gaussa dla wielomianów Legendre'a ma postać:

I (/) =

a

?

A₀f

b-a

v 2

x₀ +

a + b\ _J /b-a + - + A₃/

2 y

V

a + b\

2 y

(4 składniki, każdy odpowiada kolejnemu węzłowi od 0-wego do 3-go) c) Węzły są pierwiastkami najwyższego wielomianu ortogonalnego - u nas P4.

35

8

4    15 2    3

x--x +- = 0

4    8

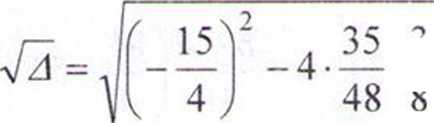
■~=slT.5

-yfi3

*0 =

X₀ =-

	{ ^11 , 4.	+ V?>5
1 2.^ 1 " 8
f \	j 4)	+ V7j

= -0.861, x, =

2-

35

8

= 0.861

15

4

2-

8

= -0,340. x₀ =

1

/

V

15

4

?.

35

8

= 0,340.

d) Współczynnik A, =

a

N

\Vn-\

, gdzie:

<*N-\ V'n

-    a,\ - współczynnik o najwyższej potędze w najwyższym wielomianie - u nas w P4, więc a,y = ³⁵/s;

-    ćf.\_i - współczynnik o najwyższej potędze w przedostatnim wielomianie - u nas w P₃, więc a\>-\ = ⁵/₂',

-    ||^v-i||² - kwadrat normy przedostatniego wielomianu, u nas Py, dla wielomianów Legendre'a

,2    2

2/ + 1

(norma liczona bez zamiany przedziałów - inaczej, niż w zad. 7! - wypada tu czynnik

a ~ b .    2

—— ),więc P₃

2-3 + 1    7

35

-    yA ~ pochodna ostatniego wielomianu (P 4) po x kolejno dla x = xo, ..X3: P\ = —x³--x,

2    2

-    y/s-t ~ wartość przedostatniego wielomianu {P₃) kolejno dlax = xo, ...,X3.

35    2

Stad A = 4    ^7    2

15

— x.---x.

A 2 ⁷

y

)

j 3    3

— x. —x

'    5xfOx?-3)(5x?-3)

2    2 j

A₀ = A(x 0) = 0,3479, A, - zł(x,) = 0.6521. A₂ = A(x₂) = 0,6521, A₃ = A(x₃) = 0,3479

\

12