DSC07299

20

Liczby zespolone

d) DIji ; = \/5 + » mamy r = 2. Sr.»d    s»u^ = j. Męc

=    ZAłm

v3- + i=2 lass

	im *	v*fl
		W
O	iU

i) DU - = ano — iceea many r = 1. Stąd eosy» = sina, sinp = -coso. Więc sf] = j = y ła. Zatem

sina - i cos a= t |cos    + aj + i sin + aj j -

0Db>= 1-ictga mamy

r = ł/l + et*³ a --=- oraz r = --(sin a — i cos cr) .

.'sino! sina    sma

2mcm = f + o. «ad ^ [cos (f + a) + isin + a)] . g*) DU •= l-f-cesa -*• i sina marny

r= y(l + ecaa)³ + sro²a = \/2(l -fcoea) =2|co8y| = 2coe —

~    a    . a / a . . a\

ZtfOBarg2= . = y.stąds = 2a»y (C08y + »sroyj.

> Przykład 1.10

SzTjsrsKzć zbiory liczb zespolonych z spełniających podane warunki:

z    2x    3t

*U^<sr8I<T' ^b)»g(* + 2-0 = »; c)_łr<arg[(-I+i>|<y;

<0 | < *8 (**)<-■ ęj.arg (;j ⁼ T^:    0y<«*.(»-*)< y-

Ror«nązanie

JU«

Argnnestem gjćw/r/m lirzby zeupokrtej x / 0 nazywamy miarę ^ kąta zorientowanego, «wxtoorgp przez drsUtrńą ezę# ow rzeczywiste} Re z oraz promień wodzący liczby z, pny 0< *< 2* *fly>-*<,,<*. ponadto argO^O.

a) Zbr> rfrta/U *» z fezb zespolonych,

KW/CB *rgor&y*y jpowne zawarte «ą

^P”^ed*^-fe(i'Tⁱ ^tOofcazarkąłow

ogranw/e/y p^rMymi wyehcdzącymi z

****** i tworzącymi kąty S i 2*

Re/ pfenrsza z tych p/Apr/sr.yrj. Ti+źy do fejy,

Przykłady

b)    Zbiór składa się z liczb zespolonych w = s — (—2-ł* i), których argumenty główne są równe ir. Jest to półprosta wychodząca z początku układu (zmienna w) i tworząca kąt jr z dodatnią częścią osi Rew. W układzie współrzędnych ze zmienną s jest to ta sama półprosta (bez początku) przesunięta o wektor za = —2 + i.

c)    W rozwiązaniu wykorzystamy wzór

arg * argzi + arg su +^k*

, ..    nierówno^

dla pewnego fc £ Z, gdzie si, za € C \ {0}. Ponieważ °^r6\    4

] 3tr

jt Ś arg[(-l + ś)zl ^ 2

jest równoważna nierówności

3x

3*

" ^ -j-+ args + 2k*ś ₂

dl

a pewnych k 6 Z. Ale 0 $ arg z < 2z\ więc k = 0. Stąd otrzymamy

x    .3*

4 ^ argz^—.

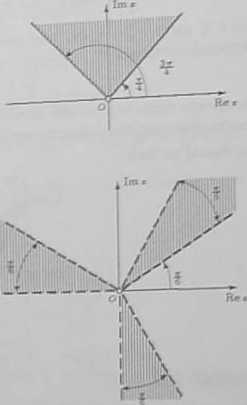
Szukany zbiór jest domkniętym obszarem kątowym ograniczonym półprostymi wychodzącymi z punktu O (bez tego punktu)

,Jt-. 3»    , , . _

i tworzącymi kąty - i — z dodatnią częścią osi Re z.

d) W rozwiązaniu wykorzystamy wzór arg [zⁿ) = n - arg z + 2kx dla pewnego k € Z, gdzie z € C oraz n € N. Nierówność _ < _arg < r jest zatem równoważna

nierówności

!<3-args + 2**Or dla pewnych fc € Z. Stąd

i

Ale 0 ^ nrgz < 2r. więc powyższa nierówność ma sens tylko dla fc = 0,fc = —I łnb k = -2. Wtedy przyjmuje ona postać

I<argz<? lub < argr < tt lub < arg* < |;r.

Szu lenny zbiór składa się z trzech otwartych obszarów kątowych (bez początku układu).