liczby zespolone 1

6

Przedstawić w postaci algebraicznej liczby zespolone:

1. z = (1 + 20(3-50    ²-*=2T3i

Rozwiązania

1.    Korzystając z faktu, że i² = — 1, mamy

z = (1 + 2i)(3 - 5i) = 3 - 5t + 6* - 10i²' = 13 + i.

2.    Mnożąc licznik i mianownik przez liczbę sprzężoną do mianownika, czyli 2 — 3i, otrzymamy

3    3(2 — 3ż)    6 — 9i 6    9 .

2 + 3» ~ (2 + 3t)(2 -30” 4 + 9 ~ 13 “ 13®

Przedstawić w postaci trygonometrycznej i wykładniczej liczbę zespoloną:

3. z =

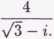
Zauważmy, że

4    4(^ + 0    AT . .

Z = —7=- = 7=-;=- = v o + Z.

\/3 — i (\/3 — 0(n/3 + 0

Aby przedstawić liczbę zespoloną w postaci trygonometrycznej, należy wyznaczyć moduł i argument, a więc

|z| = \/3 + 1 = 2, cos    , sinip=i.

Stąd = f jest argumentem liczby z, czyli z = 2 (cos f + * sin (?) jest szukaną postacią trygonometryczną, natomiast z = 2e«' jest postacią wykładniczą.

Wyznaczyć zbiór punktów spełniających nierówność:
	z — 3	< 2
4.	ź + 3

Z powyższej nierówności wynika: \z - 3| < 2\z + 3|. Niech z = x + iy, a więc ź = x - iy. Stąd mamy \x — 3 + iy\ < 2\x + 3 - iy\, czyli

V(x - 3)² + y² < 2_s/(x + 3)² + y².

Podnosząc obie strony do potęgi drugiej po uporządkowaniu, otrzymamy:

(x + 5)² + y² > 16 lub ^    > ł-

Przedstawić następujące liczby zespolone w postaci algebraicznej (kanonicznej):

1. (4 — 3i) + (2i — 6)

5. (3 + i)(3 — i) Q T. (1 - i)(2 — t)(3 - i) 9. (1 + i)²

2. (2 +1)(4 — i) -1-4 i

4.

4 — i

1 -ł- 2i 2 — i ^b' 3 - M ⁺    5i

8. (1

4    2-i

1 — i 1 + i

10.

11.

(1 + *)²

i⁴ + i⁹ + i¹⁶ 2 — i⁵ + i¹⁰ — i

1 + 2 r °

(1 + 2i)² 13. i(l + i)⁴ — (2 + i)²

12. .

1 “f ~ l 14. (1 — ż)⁶(l +i)

2

1 — i

Następujące liczby zespolone przedstawić w postaci trygonometrycznej:

15. 3	16. -4
17. -3i	18. 2 + 2\/3i
19. 1 + i	20. 1 - i
21. V3-i	22. -\/3 + i
23. —5 — 5 i	24. 1 + \/3i
25. — V2 + i\/2	^1 V3 26. --+r-
27. -\/6-iV2	28. 3 + 3\/3i
29.	1 -ł- i 30. —

1 + i