egx1

Na arkuszu papieru kancelaryjnego napisać imię i nazwisko, datę , grupę oraz tytuł. Egzamin trwa 120 minut.

1.    Wymienić symbole nieoznaczone i obliczyć nie stosując reguły de’Hospitała lim(2- x -e^x)-^r.

2.    a) Dla jakiej wartości parametru p funkcja

n

/O)

n .

x ta , x^ —

'    jest ciągła w punkcie x₀ = —

n ■    2

’ ^X ~~2

(Przy obliczaniu granicy nie stosujemy reguły de’Hospitala)

b) Sprawdzić z def., czy funkcja f (x)) z punktu a) ma pochodną

TC

w punkcie x₀ = — .(Granicę można obliczać dowolną metodą).

3.    a) Napisać wzór Maclaurina 4-tego rzędu dla /(x) = vl + x , a następnie po odrzuceniu reszty oszacować dokładność otrzymanego

7

wzoru przybliżonego dla — < x < 0 .

8

b) Napisać wzór na n-tąpochodną funkcji /(x) = M\ + x .

/    v^-2

f X

4.    Znaleźć asymptoty pionowe funkcji /(x) =

5. Znaleźć przedział, w którym funkcja /(x) =

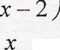
lnx

jest'¹malejąca i

wklęsła..

6. Obliczyć: a) J ^x^^nx ^ ^_x ^ ^ J.

(e^2x +2 e^x)dx

(x^z+i y

4le^x -\0-e²

=*‘> J

dx

cos x