fizyka lista nr 1

Lista zadań nr 1 dla ZIP

1.

2.

3.

4.

5.

6. 7.

8.

9.

10.

Włos ludzki rośnie z prędkością 0,4 mm na dobę. Maksymalny wiek włosa to 7 lat. Jaką długość może osiągnąć włos, którego nie będzie się ścinać przez 7 lat? Przyjmij, że rok ma 365 dni.

Serce człowieka pompuje krew z prędkością 5 litrów na minutę. Ile litrów krwi przepompuje serce w ciągu doby?

Włos o średnicy 0.1 mm ma długość 15 cm. Jaka jest jego objętość w m '?

Ziarenka piasku na plaży w Syrakuzach są drobne - na 1 mm' wchodzi 10 ziarenek. Plażę o wymiarach 50 m szerokości i 2 km długości zalega warstwa piasku grubości lOOcm. Jakiego rzędu wielkości jest ilość ziarenek piasku na tej plaży? Poletko doświadczalne ma powierzchnię równą 2500 m². Ile arów ma to poletko?

Ile sadzonek zmieści się na polu o powierzchni 112 arów, jeżeli na 1 sadzonkę przeznacza się 25 cm² powierzchni? Prędkość poruszania się ciała w ośrodku lepkim (np. w cieczy) zależy od siły działającej na ciało, jego rozmiarów oraz współczynnika lepkości danego ośrodka. Dla kulki zależność tę wyraża równanie:    F = 67tqrV, gdzie r\ -

współczynnik lepkości, r- promień kulki, V - prędkość poruszania się. Proszę wyznaczyć na podstawie tego równanie wymiar współczynnika lepkości.

Moduł Younga jest współczynnikiem sprężystości materiału, który można wyznaczyć z prawa Hoohe a przedstawianego

F " „ Al

wzorem: — - t —. gdzie F - siła odkształcająca, S - powierzchnia przekroju przedmiotu odkształcanego, E - moduł

S /„

Younga, Al - przyrost długości przedmiotu. 1₍, - długość początkowa przedmiotu. Proszę wyznaczyć wymiar modułu.

W doświadczeniu, którego celem jest wyznaczenie modułu Younga drutu uzyskano następujące wartości: F = 2 kN. r (promień drutu) = 300 pm, Al = 2,5 mm, 1₀ = 1 m. Proszę obliczyć wartość modułu Younga.

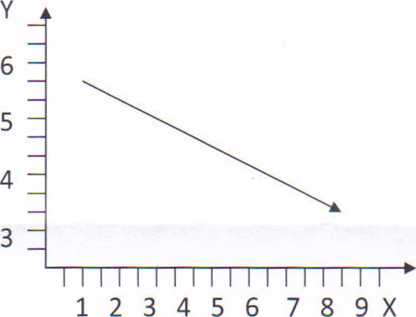
Znajdź składowe wektora przedstawionego na rysunku (zapisz przedstawiony wektor w postaci matematycznej), oraz kąt. jaki tworzy z osią X.

11.

12.

13.

14.

15.

16.

17.

18.

Wyznacz w sposób graficzny i matematyczny sumę i różnicę wektorów' A = (-5.-8) i B = (-2.7), kąt jaki tworzą te wektory z osią X, oraz kąt między nimi.

Oblicz iloczyn wektorowy i skalarny wektorów A i B z poprzedniego zadania.

Klocek o wymiarach (2 cm x 1,5 cm x 6 cm) ważący 85 g położono na płaszczyźnie nachylonej do poziomu pod kątem 30". Jaki musi być minimalny współczynnik tarcia pomiędzy klockiem i płaszczyzną aby pozostał on nieruchomy?

Kulkę o średnicy 3 cm i masie 50 g zawieszoną na nieważkiej nici o długości 70 cm wychylono o kąt 25° od pionu. Jaka jest wartość siły stycznej do nici (naprężenie nici) i normalnej do nici (kierującej kulkę do położenie równowagi)?

Jakie będzie początkowe przyspieszenie kulki z poprzedniego zadania? Czy będzie ono stałe?

Wózek o masie 2 kg poruszał się po torze płaskim bez tarcia z prędkością 4 m/s. Po przyłożeniu siły hamującej F, zatrzymał się po przebyciu drogi 8 m. Oblicz siłę hamującą.

Ciało o masie 2 kg porusza się z prędkością początkową V₀ = 0,5 m/s. W ciągu 4 sekund jego prędkość wzrasta 9-krotnie. Jaka siła działa na to ciało?

Oblicz przyspieszenie i naprężenie nici łączących elementy układu przedstawione na rysunku. Masy: mi=lkg, m₂=4kg, m-s= 2kg. Między klockiem o masie m₂ a podłożem występuje tarcie o współczynniku p = 0,2.

19. Przez krążek i momencie bezwładności 50 kgnr i promieniu 0,1 m mogący obracać się bez tarcia przełożono linę. na końcach, której zawieszono ciała o masach 3 i 5 kg. Z jakim przyspieszeniem będzie poruszał się układ? Jakie beda naprężenia nici?