IMAG0321 2

'

inputs

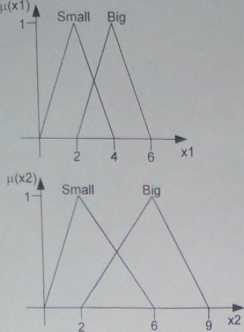
Model rozmyty realizuje wnioskowanie oparte na czterech regułach warunkowych:

1F \1 is    Smali and x2 is Smali    THEN y is    Smali

IF xl is    Smali and x2 is Big    THEN y is    Medium

IF xl is    Big and x2 is Smali    THEN y is    Medium

IF xl is    Big and x2 is Big    THEN y is    Big

Operator AND w poprzedniku reguły oraz implikacje realizowane są z zastosowaniem T'-normy typu win.

W rezultacie realizacji implikacji otrzymujemy cztery zbiory rozmyte, które są agregowane / zastosowaniem S-normy typu max, a następnie otrzymany zbiór rozmyty poddawany jest wy ostrzaniu wybraną metodą: centroid, bisektor, Iow, mom lub sow.

Realizacja w Matlabie:

Należy wprowadzić do przestrzeni Matlaba parametry trójkątnych funkcji przynależności:

» InputMF = |0 2 4;2 4 6;0 2 6;2 6 9|;

» OutputMF = |0 4 7;4 6 9;6 8 111;

/ menu Matlaka wybrać File/New/M-file i zapisać go pod nazwą MyFuzzyModel.m.

Poniżej podano M-plik funkcyjny, który należy zrealizować (nie wymagane są komentarze oznaczone %):

function out = MyFuzzyModel(xl,x2,lnputMF,OutputMF,DefuzMethod)

' o Argumenty wejściowe funkcji:

% \ 1 ,x2 - wartości zmiennych wejściowych rozmytego modelu % InputMI - parametry trójkątnych funkcji przynależności zmiennych \1 i x2 ¹o podanych w formie InputMF~[a I bl cl;a2 b2 c2;a3 b3 c3;a4 b4 c4J “o.OutputMF - parametry trójkątnych funkcji przynależności zmiennej % wyjściowej modelu podane w formie OtputMF=[al bl cl;a2 b2 c2;a3 b3 o j . DęiuzMcthod - metoda wyostrzania: 'centroid','bisector’,^,lom^,,^,mom‘ lub 'som’

% obliczenie współczynników przy należności podanych wartości xł « \2 'do zbiorow rozmytych Smali i Big____.

3