Image 107

W sytuacji kiedy P₂ = PM_P2 = 400 zł pierwsza jednostka produkcji przj stratę (KM > PM_p). Strata z produkcji drugiej jednostki wynosi zero (KM = pf i jest mniejsza aniżeli poprzednio. Trzecia jednostka produkcji przynosi zysk n to w wysokości 300 zł, czwarta w wysokości 100 zł i dopiero piąta jednostka p^ dukcji przynosi zysk netto równy zero (KM = PM_p).    ^

Dla P₂ = 400 zł zrównanie KM z PM_p następuje zarówno, kiedy Q = 2 jak i wówczas, kiedy Q = 5. Równocześnie zysk osiąga wielkość maksymalną (str ta osiąga wielkość minimalną) dla Q = 5. Jeżeli produkcja wynosi 2 jednoj krzywa zysku całkowitego (Z.) osiąga minimum miejscowe. Zwiększenie prc_ kcji o kolejną jednostkę przynosi zysk netto w wysokości 300 zł i tym samym zwiększa zysk całkowity (zmniejsza stratę).

Z obserwacji wykresu wynika, że dla Q = 2 krzywa KM jest malejąca. NiewieU kie zwiększenie produkcji powyżej 2 jednostek pozwala osiągnąć większy przy. chód dodatkowy w porównaniu z kosztem dodatkowym (PM_p > KM) - zysk całkowity rośnie (strata zmniejsza się). Niewielkie zmniejszenie produkcji poniżej Q = 2 zmniejsza bardziej koszt, aniżeli przychód - zysk całkowity wzrośnie (strata zmniejszy się). Ponieważ w odniesieniu do Q = 2 zarówno wzrost jak i spadek produkcji zwiększa zysk (zmniejsza stratę) oznacza to, że dla tej wielkości produkcji zysk osiąga minimum (strata osiąga maksimum).

(1)    Zysk osiąga maksimum, jeżeli: PM_p = KM i KM jest rosnący

(2)    Zysk osiąga minimum miejscowe, jeżeli: PM_p = KM i KM jest malejąc

Ogólnie można stwierdzić, że w sytuacji zysku dodatniego wielkością produkcji maksymalizującą zysk całkowity jest wielkość, dla której PM_p = KM i KM jest rosnący. Jeżeli zysk całkowity jest negatywny, wówczas istotnym jest porównanie rozmiarów straty z kosztem stałym całkowitym.

RÓWNOWAGA W KRÓTKIM OKRESIE CZASU

W krótkim okresie czasu oraz w warunkach rynku doskonale konkurencyjnego koszty produkcji i cena rynkowa są dla przedsiębiorstwa wielkościami danymi. Uwzględniając obydwie wielkości przedsiębiorstwo poszukuje takich rozmiarów produkcji, które maksymalizują zysk. Osiągnąwszy wielkość produk* cji maksymalizującą zysk przedsiębiorstwo znajduje się w stanie równowaflU Przedsiębiorstwo nie jest zainteresowane w zmianie wielkości produkcji, chyba że zmienią się cena lub/i koszty produkcji.

Przedsiębiorstwo znajduje się w stanie równowagi, jeśli przy danychyj kosztach produkcji i danej cenie rynkowej wytwarza wielkość produkcji J| maksymalizującą zysk

one optimum i równowagi przedsiębiorstwa są ze sobą ściśle powiązane.

Kateg u _c dotychczasowe przykłady liczbowe dotyczące cen i kosztów pro-Vty^korZ^_nalizujemy różne sytuacje równowagi przedsiębiorstwa. W celu osiąg-dukeji ^za _kszej przejrzystości analizy posłużymy się wykresem, na którym obok pjęcia ^w,^_osztu marginalnego (KM) zaznaczymy również krzywe kosztów prze-^k^fych obliczone na podstawie dotychczasowych danych (wykres 104).

Wykres 104. Równowaga

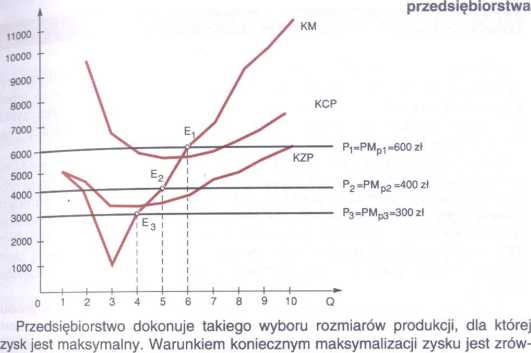
nanie się PM_p z KM, natomiast warunkiem wystarczającym jest to, aby KM był rosnący. Spoglądając na wykres 104 zauważamy, że wszystkie trzy punkty E„ E₂ i E₃ odpowiadające różnym cenom rynkowym spełniają wymogi maksymalizacji zysku. O ile jednak w przypadku ceny P₁ i P₂ przedsiębiorstwo może funkcjonować i oferować na rynek odpowiednie wielkości produkcji, o tyle w sytuacji ceny P₃ = 300 zł przedsiębiorstwo powinno zaprzestać produkcji w ogóle.

Jeżeli cena rynkowa wynosi P, = 600 zł, wielkość produkcji maksymalizująca zysk wynosi 6 jednostek. Równocześnie dla Q = 6 cena jest większa od kosztu całkowitego przeciętnego (P, > KCP). Oznacza to, że zysk jednostkowy a także ²ysk całkowity jest dodatni. Punkt E, jest punktem równowagi przedsiębiorstwa.

W przypadku ceny rynkowej P₂ = 400 zł produkcją maksymalizującą zysk jest ^Q = 5. Dla tej wielkości produkcji cena jest niższa od kosztu całkowitego przekątnego (P₂ < KCP). Oznacza to, że przedsiębiorstwo osiąga zysk ujemny

^ratę). Równocześnie jednak P₂ > KZP co oznacza, że przychód jednostkowy .®^na) pokrywa koszt zmienny przeciętny i część kosztu, stałego. Wytwarzając kos^6rU^^{C na} ^^nek Q ^{= 5} przedsiębiorstwo osiąga stratę, która jest mniejsza od zio ^{2tU stałe}9° całkowitego. E₂ jest punktem równowagi przedsiębiorstwa a po-_Ujem ^Produkci' Q = 5 minimalizuje stratę przedsiębiorstwa (maksymalizuje zysk

215