Image 41

Między przychodem przeciętnym, który równy jest cenie, a przychodem marginalnym istnieje taka zależność, że obydwie wielkości zmniejszają się, przy czym przychód marginalny spada szybciej aniżeli przeciętny. Wynika to z faktu iż cena (równa przychodowi przeciętnemu) jest zawsze większa od przychodu marginalnego.

Istnieje związek między przychodem marginalnym i cenową elastycznością popytu. Przypuśćmy, że cena spada z Pi do P₂ (P₂ < Pi) natomiast sprzedaż wzrasta o jednostkę z QD do QD + 1.

Przychód całkowity ze sprzedaży po cenie Pi wynosi:

PC_pi = Pi • QD

Przychód całkowity ze sprzedaży po cenie P₂ wynosi:

PC_p2 = P₂ • (QD + 1)

Przychód marginalny ze sprzedaży dodatkowej jednostki produktu jest różnicą przychodów całkowitych i wynosi:

PM_p = PC_p2 - PC_p1 = P₂ • (QD + 1) - Pi ■ QD =

= P₂ • QD + (P₂ • 1) - PiQD = P₂ • 1 + QD • (P₂ - Pi)

Ponieważ P₂ jest mniejsze od Pi różnica P₂ - Pi jest liczbą ujemną. Przychód marginalny jest równy nowej, niższej cenie P₂ minus pewna wielkość. Dlatego właśnie cena jest większa od przychodu marginalnego: P₂ > PM_p.

Traktując zmiany QD jako dyskretne, tzn. zmiany o jedną jednostkę, możemy ogólnie zapisać, że:

PMp = P - AP • QD - w przypadku wzrostu ceny PMp = P + AP • QD - w przypadku spadku ceny.

Uwzględniając inne, dowolnie małe zmiany sprzedaży w przyroście sprzedaży AQD, wzór na przychód marginalny zapiszemy:

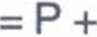
APQD

AQD

Mnożąc prawą stronę powyższego równania przez P/P otrzymujemy:

( AP >		f^QDV	^rp)
^ AQD /		l p J	UJ

lub inaczej

f

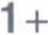
AP

AQD

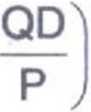
Dla krzywej popytu o nachyleniu negatywnym E_P jest zawsze liczbą ujemną. W rezultacie zawsze kiedy 1/E_P * 0 całe wyrażenie będzie ujemne, a wartość wyrażenia w nawiasie będzie mniejsza od jedności. Wynika stąd, że zawsze p > PMp.

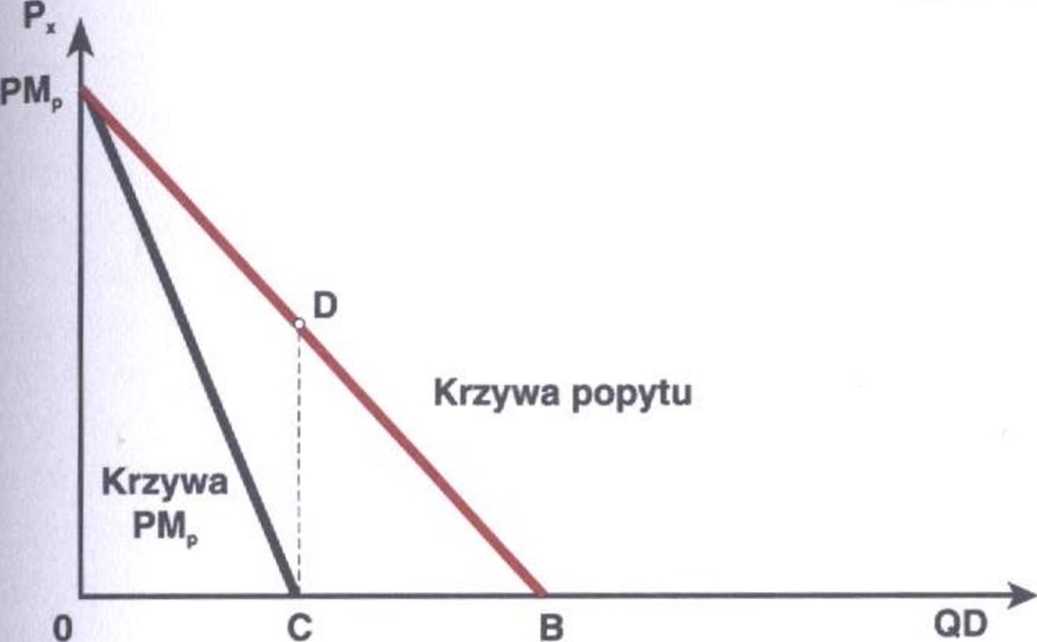
Graficzną prezentację krzywej przychodu marginalnego zawiera wykres.

Wykres 33. Krzywa przychodu

Ponieważ elastyczność cenowa popytu wynosi: E_p

AQD

AP

P

QD’

stąd:

PM

p

/

= P

1 +

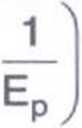
marginalnego

W punkcie D znajdującym się w połowie krzywej popytu E_p = - 1. Podstawiając wartość E_P = - 1 do wzoru na PM_P otrzymujemy

= P

/

1 +

\

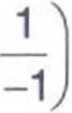
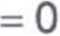
Dla kombinacji cena - wielkość popytu znajdującej się w punkcie D na krzywej popytu przychód marginalny równa się zero.

W punkcie A krzywa popytu przecina oś rzędnych. Elastyczność cenowa popytu w tym punkcie wynosi - co, a przychód marginalny wynosi:

/

= P

1 +

—00

= P(1 + 0) = P

(każda liczba dzielona przez oo równa się zero). W punkcie przecięcia się krzywej popytu z osią rzędnych przychód marginalny równa się cenie.

Elastyczność cenowa popytu	Przychód marginalny
IEPI = 1	PMp = 0
lEpl > 1	O A Cl 2 CL
lEpl < 1	PMp < 0

83