Image 73

ka zmiennego - początkowo wzrasta coraz szybciej, później natomiast coraz wolniej. Zmiany PC przedstawia wykres 63.

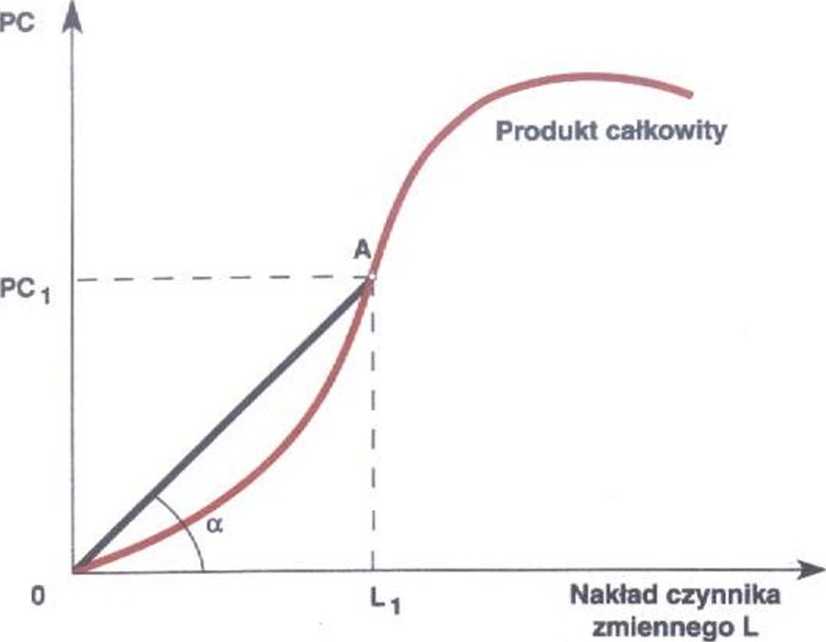
Wykres 63. Przebieg krzywej produktu całkowitego (PC)

Posługując się krzywą produktu całkowitego możemy wyznaczyć produkt przeciętny (PP). Przykładowo nakładowi czynnika zmiennego OL, odpowiada wielkość produkcji OPC_r Z definicji produktu przeciętnego wynika, że jest on stosunkiem: OPC/OL, = L^OL,. Równocześnie wiadomo, że relacja L^OL, stanowi nachylenie linii prostej łączącej punkt A z początkiem układu.

PP_L = L,A/OL układu = tg a

W miarę zwiększenia nakładu czynnika zmiennego zmienia się również produkt przeciętny - początkowo produkt przeciętny wzrasta, a później, po osiągnięciu maksimum, zaczyna spadać. Kształtowanie się produktu przeciętnego możemy wyprowadzić z geometrycznej analizy krzywej produktu całkowitego (wykres 64).

Wykres 64. Geometryczne wyznaczanie zmian

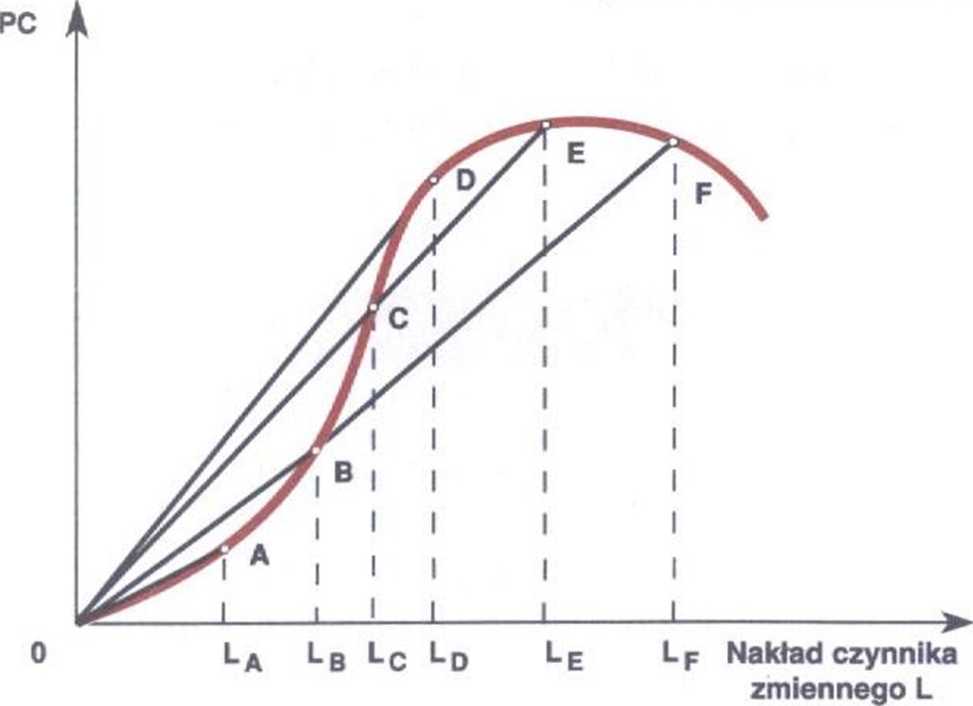
produktu przeciętnego

Zwiększając nakład czynnika zmiennego do 0 od L_A, do do l__F otrzymujemy odpowiednio punkty A, B, C, D, E, F na krzywej produktu całkowitego.

żącząc te punkty z początkiem układu otrzymujemy linie proste, których nachylenie wzrasta do punktu D, a następnie maleje.

Tak więc produkt przeciętny (równy nachyleniu linii prostej) wzrasta do rozmiarów L_d nakładu czynnika zmiennego (punkt D na krzywej produktu całkowitego), a następnie zaczyna spadać. W punkcie D produkt przeciętny osiąga maksimum.

W podobny sposób wyznaczamy produkt marginalny, który wyraża stosunek zmiany produktu całkowitego do jednostkowej zmiany nakładu czynnika zmiennego. Traktując zmiany nakładu czynnika zmiennego jako nieskończenie małe produkt marginalny możemy wyrazić jako nachylenie krzywej produktu całkowitego w danym punkcie tej krzywej. Produkt marginalny wyznaczamy przy pomocy nachylenia linii stycznej do danego punktu na krzywej produktu całkowitego (wykres 65).

Wykres 65. Geometryczne wyznaczanie zmian

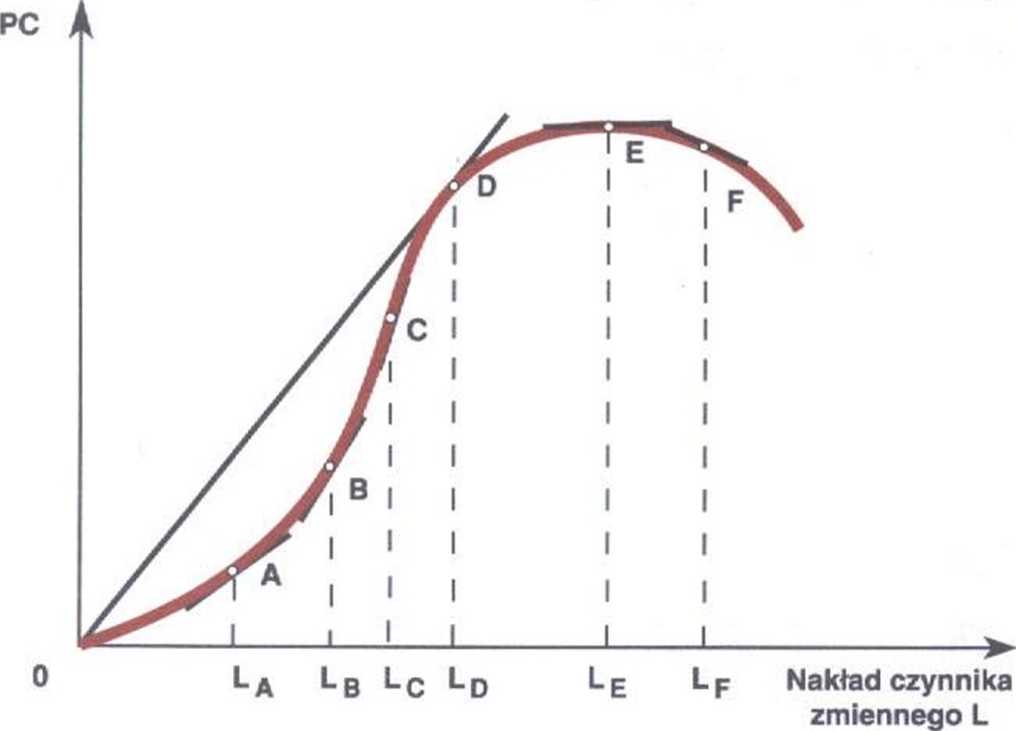
produktu marginalnego

Nachylenie stycznych najpierw rośnie, a później spada. Po przekroczeniu punktu E nachylenie przybiera wartość negatywną.

Analizując zmiany nachylenia stycznych, czyli zmiany produktu marginalnego, należy zwrócić uwagę na trzy charakterystyczne momenty:

-    nachylenie stycznej (produkt marginalny) rośnie aż do pewnego punktu (punkt C), a następnie zmniejsza się. Jest to punkt przegięcia krzywej produktu całkowitego. W punkcie tym produkt marginalny jest największy,

-    styczna do punktu D przechodzi równocześnie przez początek układu. Oznacza to, że właśnie w tym punkcie (jedynym na krzywej produktu całkowitego) produkt przeciętny jest równy produktowi marginalnemu. Wiemy również, że w punkcie D produkt przeciętny osiąga swoje maksimum,

-    w punkcie E nachylenie stycznej jest zerowe, czyli produkt marginalny równa się zero. Po przekroczeniu punktu E nachylenie stycznej jest negatywne (np. punkt F) co oznacza, że produkt marginalny staje się ujemny.

147