image 2

Gęstość rozkładu zmiennej losowej X jest dana wzorem

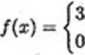
(Zx² dla 0 < x < 1,

\0 dla pozostałych x.

Dla zmiennej losowej Y — e~^x znaleźć

a)    EY,

b)    dystrybuantę.

Zmienna losowa X ma dystrybuantę

e^-rJ dla x < 0, 1 dla x > 0.

Obliczyć Pr(-e < Y < -e^-1) oraz gęstość zmiennej losowej Y = c~^x.

Pomieszczenie jest oświetlone za pomocą dwóch żarówek pracujących niezależnie. Czasy świecenia żarówek X i Y mają rozkład wykładniczy z parametrem A. Niech T oznacza moment uszkodzenia ostatniej sprawnej żarówki. Wyznaczyć:

a)    dystrybuantę zmiennej T,

b)    gęstość zmiennej T,

c)    ET,

d)    D^?T.

5