IMAGE0139

128

Jeśli z punktami brzegowymi wiążemy jednorodny warunek kinematyczny na wartość funkcji ugięcia, to dla tego punktu nie piszemy równania różnicowego. Dla analizowanej belki zapiszemy więc cztery równania dla ;=1,2,3,4

128

-j -4v,_| +6v, - 4v,^, +v._t2

A⁴

(6.8)

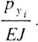
Możemy po lewej stronie równań pozostawić jedynie licznik ilorazu różnicowego i wówczas w równaniach po prawej stronie pojawią się niezerowe wyrazy wolne, wyznaczone dla przypadku p_v,^t 0 w postaci

B, =

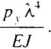
(6.9)

Układ równań w zapisie macierzowym ma postać

A V = B ,    (6.10)

(8x8) (8x1)    (8x1) gdzie wektor V zawiera niewiadome wartości ugięć węzłów.

Dla przykładu zapiszemy równanie różnicowe dla punktu pierwszego (i=l)

(+1) ■ v_, + (-4) • v₀ + (+6) ■ v, + (-4) ■ v₂ + (+1) • v₃ = B_t = B .

Postulowane warunki brzegowe dla obu końców belki wspornikowej (zapisane dla węzłów ;'=0 oraz i=4) sprowadzają się do następujących równań algebraicznych:

v₀ = 0 .

^vo =^r(-^y-i +v₊₁) = 0-K-l)-v_, +(+l)v₊₁ =0, EJ

M_l =-EJv_l =-—(v₃ -2v₄ +v₅) = 0->

A

(— 1) - v₃ + (+2) • v₄ +(—!)• v₅ = 0,

^Tl =-£/v" = -^-(-v, + 2v_}-2v_s + v₆) = 0-

(+l)-v, + (-2) • v_, + (+2) • v₅ +(-l)-v₆ = 0.

Równania te dołączymy do powyżej zapisanych czterech równań (6.8), otrzymując łącznie N= 8 równań o 8 niewiadomych ugięciach v, dla i - -1,0,....6

(L) = 0.125-

6		^V-1
8		^vo
5		^vi
5	, v =	^V2
0
0
0		^V5
0		_^V6 .

(6.11)

1	-4	6	-4
0	1	-4	6
0	0	1	-4
0	0	0	1
0	1	0	0
-1	0	1	0
0	0	0	0
0	0	0	+ 1

1	0	0	0
-4	1	0	0
6	-4	1	0
-4	6	-4	1
0	0	0	0
0	0	0	0
-1	2	-1	0
-2	0	+ 2	-1

Rozwiązaniem układu równań, dotyczącego belki z obciążeniem ciągłym, jest następujący wektor V:

V = { 4.05 0.0 4.05 12.55 23.05 34.05 45.06 56.56} ,

gdzie

5 = p^/EJ ■

Jako kontrolną wielkość przyjmiemy ugięcie na swobodnym brzegu x = L. Wynik otrzymany po zastosowaniu MRS skonfrontujemy z wynikiem analitycznego rozwiązania podanego w p.4.2.3.

py^L

EJ

,^MRS(L) = v₄=34 -^Py

X⁴

EJ

= 34-

Py

EJ

0.133

pX

EJ

= 1.064-v^anali,( L).

Dla analizowanej belki, obciążonej równomiernie, obliczymy dodatkowo moment zginający przykładowo dla węzła i'=0 (brzeg utwierdzony), korzystając z równań różnicowych

( Py
	UJJ

M₀ =-EJvó=-y<v._l - 2v₀ + v,) = ~EJ\ _T | (4.0-0.0 +4.0>

W przypadku II belki obciążonej skupioną siłą pionową P , przyłożoną do swobodnego końca, jedynym różnym od zera wyrazem wolnym jest element 5_S, wynikający z warunku brzegowego