IMG00045

3. Stateczność prętów ściskanych lub zginanych oraz sprężyn śrubowych

W obliczeniach wstępnych można korzystać z prostego wzoru

a =

(3.9)

gdzie: F_br - pole przekroju poprzecznego pręta brutto (tj. bez odliczania otworów na nity, śruby itp), /?-współczynnik wyboczeniowy, którego wartości należy odczytać z tabl. 3.2 dla stali i staliwa, z tabl. 3.3 zaś dla żeliwa, stopów aluminium i drewna.

3.2. Wyboczenie prętów dwugałęziowych i wielogałęziowych o przekroju stałym

Dla prętów o przekroju stałym, złożonych z dwu lub kilku prętów połączonych ze sobą przewiązkami (rys. 3.2) lub kratą (rys. 3.3), obliczenia na wyboczenie należy przeprowadzać zgodnie z normą [38], Zasadniczym elementem obliczeń jest analiza tego, by nie nastąpiło wyboczenie pręta (słupa) o przekroju złożonym, traktowanego jako całość, jak również wyboczenie każdej gałęzi pręta na odcinkach między przewiązkami lub węzłami kraty.

Smukłość każdej gałęzi pręta należy obliczać jako iloraz długości gałęzi na odcinku między przewiązkami lub węzłami kraty przez promień bezwładności i przekroju względem osi, oznaczony na rys. 3.2 i 3.3 cyframi 1-1.

Smukłość całego pręta należy obliczać ze wzoru

s'_y = s_yy    (3.10)

gdzie s_y - smukłość całego pręta względem osi y-y według rys. 3.2 i 3.3

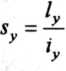
ly - długość wyboczeniowa w kierunku prostopadłym do osi y-y według rys. 3.2 i 3.3, i_y - promień bezwładności całego przekroju (tj. wszystkich gałęzi) względem osi y-y.

a)

b)

C) ry TT\r

-f

1

4j-"h iT

<jgpg,. ifojagi

l-«—e —►!

y^1		Li
«Z27ZZ&
		/	X
		r

fi^lL If!_v

I

i

Rys. 3.2

45