IMG00218

II. Obliczenia wytrzymałościowe w przypadku obciążeń zmęczeniowych

cr.

max

(17.1)

gdzie: cr_max - naprężenie maksymalne związane z istnieniem zmian kształtu przedmiotu, a„ - naprężenie nominalne obliczone z konwencjonalnych wzorów wytrzymałościowych dla najbardziej osłabionego przekroju przedmiotu (w przypadku skręcania lub ścinania - odpowiednio r_max i r„).

Wartości współczynnika kształtu a_k dla zmian przekroju najczęściej spotykanych w budowie maszyn, ujęte w formie wykresów, podano w rozdz. 18 (rys. 18.11-f 18.45).

Aby wyznaczyć współczynnik kształtu a_k za pomocą wymienionych wyżej wykresów, należy m.in. znać promień dna karbu p, tj. minimalny promień w miejscu nagłej zmiany kształtu przedmiotu. W przypadku ostrych podcięć promień oblicza się ze wzoru

(17.2)

p = p_k + p_m

przy czym: p_k - promień rzeczywisty (konstrukcyjny) dna karbu, p_m - promień minimalny dna karbu (wartość tego promienia należy odczytać z wykresu podanego na rys. 18.8).

Jak wynika z rys. 18.8, dopiero dla dostatecznie dużych promieni dna karbu, gdy p_k> 5 mm, promienia minimalnego p_m można nie uwzględniać, przyjmując

Pk = Pm

17.1.3. Współczynnik działania karbu /?*

Spiętrzenia naprężeń określonego współczynnikiem a_k [wzór (17.1)] przy działaniu obciążeń stałych w ogóle się nie uwzględnia w obliczeniach wytrzymałościowych, natomiast w przypadku obciążeń zmiennych spiętrzenie naprężeń powoduje dość istotne zmniejszenie wytrzymałości przedmiotu.

Stosunek wytrzymałości zmęczeniowej próbek gładkich bez karbu (Z_bk) do wytrzymałości zmęczeniowej próbek gładkich z karbem (Z_k) określa się tzw. zmęczeniowym współczynnikiem działania karbu lub krócej - współczynnikiem karbu fi_k

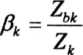
(17.3)

Pomeważ współczynnik karbu fi_k zależy od właściwości materiału, przeto wprowadzono tzw. współczynnik rj wrażliwości materiału na działanie karbu lub krócej współczynnik wrażliwości, określony wzorem

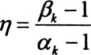
(17.4)

216