IMG00224

II. Obliczenia wytrzymałościowe w przypadku obciążeń zmęczeniowych

Naprężenia minimalne cr,^ = O, a naprężenia średnie

II. Obliczenia wytrzymałościowe w przypadku obciążeń zmęczeniowych

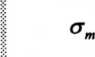
64 + 0 2

= 32 MPa

Amplituda cyklu ma wartość

-er.

64-0

= 32 MPa

Istotną sprawą jest ustalenie, jak zmieniają się wartości cr_m i cr_a przy zmianie (wzroście) obciążenia. Ponieważ siła obciążająca płaskownik, wzrastająca od zera do P_mm, jest siłą tętniącą, wydaje się więc, że zwiększenie obciążenia płaskownika może nastąpić poprzez wzrost siły P_mm, przy zachowaniu wartości minimalnej równej zeru. Przy zmianie obciążenia zmieni się zarówno wartość cr_max, jak też naprężeń średnich cr_m i amplitudy cr_a, natomiast stosunek <7_m/cr_a = 1 pozostanie wartością stałą: cr_m/cr_a - const.

Jest to więc cykl o stałym stosunku naprężeń średnich do amplitudy i dla obliczenia zmęczeniowego współczynnika bezpieczeństwa skorzystamy ze wzoru (17.18)

x

Pr°a +°n

Wartości wytrzymałości zmęczeniowej dla stali St3 przy różnych cyklach znajdujemy w tabl. 19.4

Z_ro = 130 MPa, Z_n = 210 MPa

Obliczymy następnie wartość współczynnika spiętrzenia naprężeń ze wzoru (17.8)

p = [\ + rj(a_k-\)\p_p

gdzie: P_P - współczynnik stanu powierzchni (rys. 18.6). Dla stali St3 o wytrzymałości doraźnej na rozciąganie R_r = 400 MPa i dla 5 klasy chropowatości powierzchni P_p= 1,1; rj - współczynnik wrażliwości materiału na działanie karbu (rys. 18.9). Dla stali St3 o Z_go - 170 MPa, w stanie surowym, r] - 0,66; a_k - współczynnik kształtu dla rozciąganego płaskownika z otwo-

30

rem. Dla stosunku dlb = — =0,475 z wykresu na rys. 18.38 odczytano

63

a_k = 2,2.

Współczynnik spiętrzenia naprężeń wynosi więc

224