IMG00236

II. Obliczenia wytrzymałościowe w przypadku obciążeń zmęczeniowych

liczba cykli

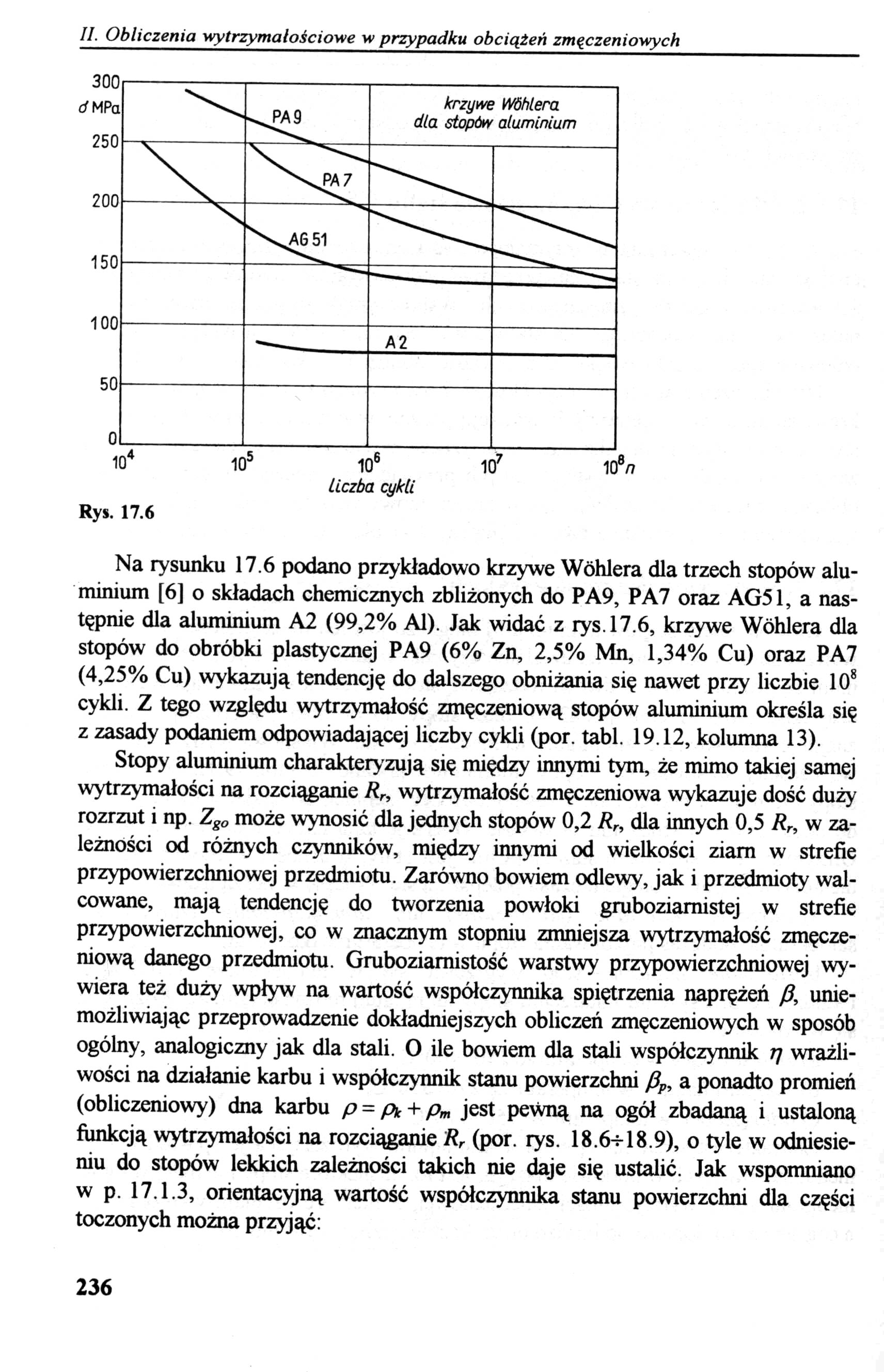
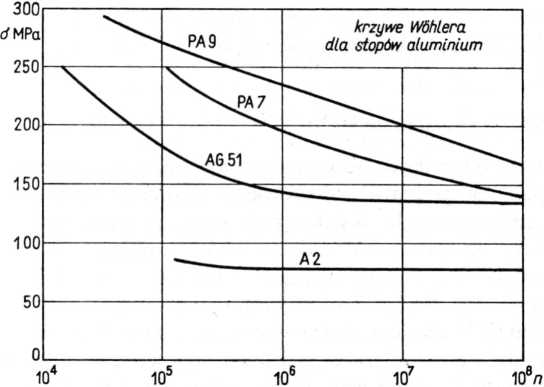
Rys. 17.6

Na rysunku 17.6 podano przykładowo krzywe Wóhlera dla trzech stopów aluminium [6] o składach chemicznych zbliżonych do PA9, PA7 oraz AG51, a następnie dla aluminium A2 (99,2% Al). Jak widać z rys. 17.6, krzywe Wóhlera dla stopów do obróbki plastycznej PA9 (6% Zn, 2,5% Mn, 1,34% Cu) oraz PA7 (4,25% Cu) wykazują tendencję do dalszego obniżania się nawet przy liczbie 10⁸ cykli. Z tego względu wytrzymałość zmęczeniową stopów aluminium określa się z zasady podaniem odpowiadającej liczby cykli (por. tabl. 19.12, kolumna 13).

Stopy aluminium charakteryzują się między innymi tym, że mimo takiej samej wytrzymałości na rozciąganie R_r, wytrzymałość zmęczeniowa wykazuje dość duży rozrzut i np. Z_go może wynosić dla jednych stopów 0,2 R_r, dla innych 0,5 R_r, w zależności od różnych czynników, między innymi od wielkości ziam w strefie przypowierzchniowej przedmiotu. Zarówno bowiem odlewy, jak i przedmioty walcowane, mają tendencję do tworzenia powłoki gruboziarnistej w strefie przypowierzchniowej, co w znacznym stopniu zmniejsza wytrzymałość zmęczeniową danego przedmiotu. Gruboziamistość warstwy przypowierzchniowej wywiera też duży wpływ na wartość współczynnika spiętrzenia naprężeń /?, uniemożliwiając przeprowadzenie dokładniejszych obliczeń zmęczeniowych w sposób ogólny, analogiczny jak dla stali. O ile bowiem dla stali współczynnik 17 wrażliwości na działanie karbu i współczynnik stanu powierzchni fi_p, a ponadto promień (obliczeniowy) dna karbu p = p* + p_m jest pewną na ogół zbadaną i ustaloną funkcją wytrzymałości na rozciąganie R_r (por. rys. 18.6+18.9), o tyle w odniesieniu do stopów lekkich zależności takich nie daje się ustalić. Jak wspomniano w p. 17.1.3, orientacyjną wartość współczynnika stanu powierzchni dla części toczonych można przyjąć:

236