IMG00230

11. Obliczenia wytrzymałościowe w przypadku obciążeń zmęczeniowych

17.4.2. Obliczenia wytrzymałościowe w przypadku zmęczeniowego działania naprężeń normalnych i naprężeń stycznych

W przypadku jednoczesnego działania naprężeń normalnych a od rozciągania, ściskania lub zginania oraz naprężeń stycznych r od skręcania lub ścinania obliczenia zmęczeniowe sprowadzają się do sprawdzenia warunku (por. [17], rozdz. 4)

>x„

=

i

4+4

(17.28)

gdzie: x_zr - współczynnik bezpieczeństwa dla rozciągania (lub zginania czy ściskania) obliczony ze wzoru (17.10) (gdy występuje cykl symetryczny) lub ze wzorów (17.18)-K17.20) (dla cykli niesymetrycznych); x_a - współczynnik bezpieczeństwa dla skręcania (lub ścinania), obliczony ze wzorów (17.10) lub (17.18)-r(17.20), w których zamiast naprężeń normalnych cr należy wstawić naprężenia styczne r.

Przykład 17.3. Obliczyć zmęczeniowy współczynnik bezpieczeństwa dla | wału skręcanego i zginanego, przedstawionego na rys. 17.4. Moment gnący wynosi M_g = ±2000 N-m, a moment skręcający zmienia się od zera do M_s = 4500 N-m. Wał jest wykonany ze stali St35 w stanie normalizowanym.

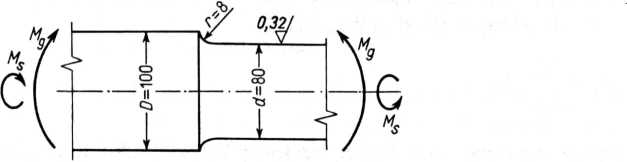
Rys. 17.4

Rozwiązanie. Dla obustronnie zmiennego cyklu zginania wału naprężenie średnie cr_mg = 0, a amplituda naprężeń

°gmax

M„ 32 M₀ 32-2000-10³ g_ _x zuuu iu _{=39 8Mpa}

W

7C d

Tt-80"

Dla jednostronnie zmiennego cyklu skręcania naprężenie średnie r_m równe jest amplitudzie z_a i równe połowie naprężeń maksymalnych

1    1 \6M_S    16-4500-10³

r_n = v_a =-r_max =--r— ⁼--—w22,4 MPa

2    2 tid³ 2ti-80³

Własności wytrzymałościowe stali St35 są następujące (według tabl. 19.5):

230