img064 2

2.    W odniesieniu do poszczególnych wyciętych myślowo węzłów kratownicy zapisuje się dwa równania równowagi: XX = 0, XY = 0. W węźle zakłada się, ż_e siły w prętach mają zwroty odpowiadające rozciąganiu prętów (od węzła) W wypadku kratownicy mającej w węzłów można zapisać 2w równań równowagi Jeśli składowe reakcji podpór wyznaczy się z trzech równań równowagi, to spośród 2w równań dotyczących węzłów tylko 2w —3 równań będzie niezależnych, a pozostałe będą spełnione tożsamościowo i mogą być wykorzystane do sprawdzenia obliczeń.

3.    Z zapisanych równań równowagi wyznacza się niewiadome siły we wszystkich prętach kratownicy. Najlepiej rozpocząć od rozwiązywania równań dotyczących węzła, w którym zbiegają się tylko dwa pręty o nieznanych silach, a następnie rozpatrywać równania odnoszące się do kolejnych węzłów spełniających ten warunek. Taki sposób postępowania znacznie ułatwia rozwiązanie.

Jeśli niezbędne jest wyznaczenie sił wyłącznie w wybranych prętach kratownicy, to wygodne jest zastosować metodę przekrojów (Rittera). Stosując tę metodę kolejno wykonuje się niżej omówione czynności.

1.    Z równań równowagi wyznacza się składowe reakcji podpór kratownicy.

2.    Prowadzi się przekrój a —a przez trzy pręty kratownicy nie zbiegające się w jednym punkcie, w tym przez pręt (lub pręty), w którym siłę należy wyznaczyć. Część kratownicy oddzielona przekrojem a —a znajduje się w równowadze pod działaniem sił zewnętrznych, składowych reakcji podpór oraz sił w prętach, przez które poprowadzono przekrój.

3.    W odniesieniu do wydzielonej części kratownicy zapisuje się równania sumy momentów wszystkich sił względem trzech punktów, w których przecinają się parami kierunki poszukiwanych sił w prętach. Punkty te są nazywane punktami Rittera. Z trzech zapisanych równań równowagi oblicza się siły w trzech prętach. Jeżeli dwa z prętów, przez które poprowadzono przekrój a —a, są do siebie równoległe, to zapisuje się dwa równania sumy momentów wszystkich sil działających na część kratownicy względem punktów, w których trzeci pręt przecina się z prętami równoległymi, oraz trzecie równanie sumy rzutów wszystkich sił na oś prostopadłą do kierunku prętów' równoległych.

Przykład 4-6. Obliczyć metodą analitycznego rówmoważenia węzłów siły w prętach kratownicy przedstawionej na rys. 4-9a.

Równania równowagi rozpatrywanej kratownicy:

XX = H_a + Pj cosa = 0,

XY = V_A + R_B-P_lsinz — P₂-P_} = 0,

XM_b = V_A- 6.0 +P, cosa - 3,0- P_{ sina-6.0-P, • 3,0+ P₃ • 3,0 = 0.

Z tych równań otrzymuje się:

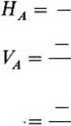
P, cosa = -40 0,707 = -28,28 kN,

P, cosa - 3,0 +P, sina - 6,0 +P₂ • 3,0 —P₃ • 3,0

6J)    ⁼

40 • 0,707 • 3,0 + 40 ■ 0.707 • 6,0 + 30 • 3,0 - 20 • 3,0

6,0

= 19,14 kN,

a = U 5° cosor = 0,707 sincr =0,707

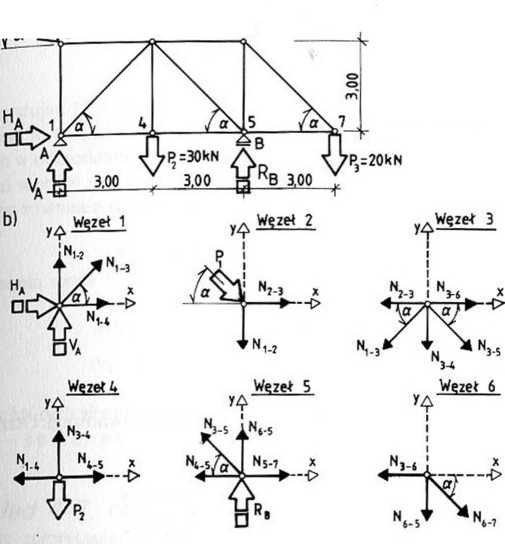
Rys. 4-9

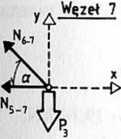
R„ = Pi sina+P₂ + P₃ - V_A = 40 • 0,707 + 30 + 20 - 19,14 = 59,14 kN.

Równania równowagi poszczególnych węzłów (rys. 4-9b) mają postać:

a)    węzeł 1

ZX = H_A + N,_₃cosa + N_l_₄ = 0,

ZY= V_a + N,__: + N,_₃ sina = 0,

^b)    węzeł 2

ZX = P, cosa +N,_₃ = 0.

ZY= — P, sina —iV,_₂ = 0,

^c)    węzeł 3

ZX = —N₂_₃ — N_l_₃cosx + N₃__(j + N₃_₅cos<x=0,

ZY= —N,_₃sinot — N₃_₄ — N₃__ssinx - 0,

^Mecluuiilta konstrukcji    113