img133

W celu umożliwienia zastosowania równań trzech momentów (12-4), podporę plas^. C (utwierdzenie) zastąpiono podporą przegubową oraz dodano przęsło CC₀ o sztywność EI_CCo = oo, co jest równoznaczne z przyjęciem l_cc = 0.

Równania trzech momentów (12-4) zapisano w postaci zależności:

M_Al'_AB + 2 M_B(l_AB + Ibc) + M_c1_Bc--6(śf'_nA + £%'bc)>

M b^bc + 2 M_c(Ibc + IćcJ + M cjcc„ = — 6(1®Ćb + ^?Ćc₀)>

w których (por. tabl. 14-30; schematy belek rzeczywistych, które przyjmuje się do obliczeń reakcji wtórnych, pokazano na rys. 12-1 lc):

®bc =

M'ba = EIab

1'ab — IaB rr    ^ AB ^ ^m>

El ab

^l'^BC = ,BC £V ⁼ 1bcU ^{= 8} 2 ^{= 4 m}’

^EIab = o_Aba =    - 45,00 kN • m²,

El

AB

El

BC

21

16

BC

2    24

10-8³

48

= 106,67 kN-m²,

•#cb = 106,67 kN ■ m², 0t'_CCa = 0, l'_CCa = 0.

o)

| =10kN

lP:20kN

p:10kN/m

kZ_V_		inninnnfinffliHin! ?
1 2 L-U	^ 2 LU 4 3 l 3	^ nn ćw
	6	t---^8-i

zginający nad podporą A

Moment

M_a = -P,-2 = -20 kN-m.

po P°

Ustawieniu powyższych danych równania trzech momentów będą miały postać:

6-(-20) + 20M_B + 4M_c = -6(45,00+106,67)= -910, 4M_B + 8M_C = -6-106,67 = -640.

1 równań tych otrzymuje się:

M_b= -26,11 kN-m, M_c = -66,95 kN• m.

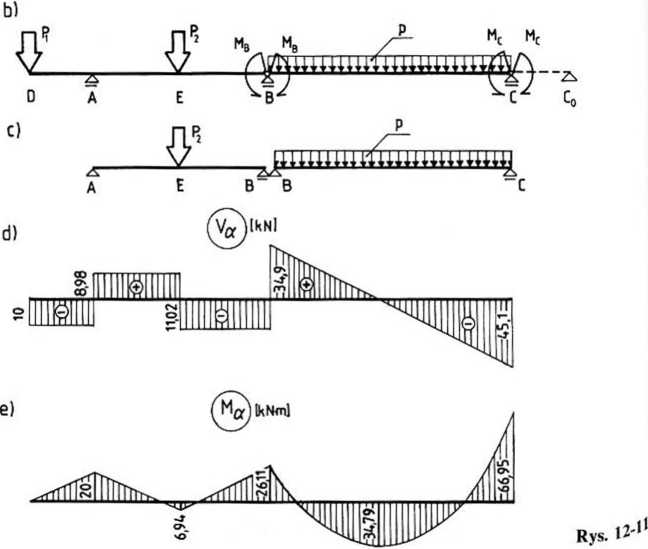
Wartości reakcji wynoszą (por. rys. 12-1 lb):

R_a = 18,98 kN, R_ba = 11,02 kN,

R_b = 45,92 kN, R_bc = 34,90 kN, R_c = 45,10 kN.

Wykres sił poprzecznych V_a przedstawiono na rys. 12-1 ld, a wykres momentów zginających na rys. 12-1 le.

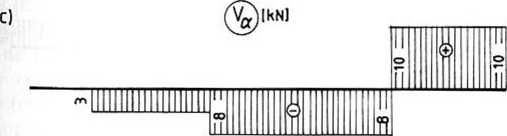
Przykład 12-9. Sporządzić wykresy sił poprzecznych V_x i momentów zginających M_x w belce jak na rys. 12-12a.

Belka jest jednokrotnie statycznie niewyznaczalna.

Równanie trzech momentów ma postać

MaIAb "h 2Mb{1Ab + ^bc) + McIbc — o) M=20kNm r*	-m,	9 A +-^Bc)-P=10kH^
Si >:* * ? .	-c	Ł ^2
b) W	Ą	-T" ty
^-1 t	c	2