img024 2

>» Wykład z fizyki «<

Niech będzie dany układ punktów materialnych m_t m_2ł ... , m_n i niech r_]9F₂^._yr„ oznaczają wektory wodzące tych punktów w dowolnym układzie współrzędnych x, y. z.

Środkiem masy tego układu punktów nazywamy punkt, którego wektor wodzący

Z m,r_t

-    (6.4)

Z ^mi

1*1

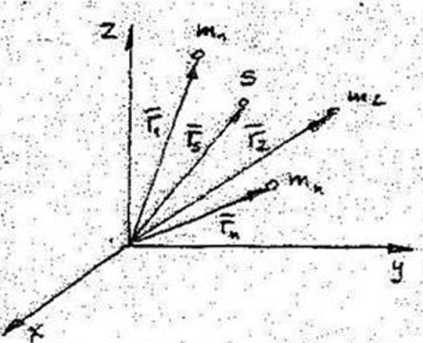
Współrzędne środka masy mają postać:

Z ^m<^xi

n

Z ^m,y,

X = ~

i!

Z «i

/=1

Z «,^zi

^---(6.5)

Z

;«1

»> Wykład i fizyki «<

W przypadku ciała sztywnego, zamiast sum we wzorze (6.4) występują całki będące granicami tych sum, gdy masy elementów dm, na które podzielono masę ciała sztywnego dążą do zera.

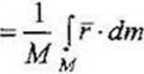
(6.6)

Gdzie M jest masą ciała sztywnego.

Element masy dm = p-dV_t gdzie ^p jest gęstością elementu dm. Podstawiając tę tożsamość do wzoru (6.6) otrzymujemy:

Oraz:

f=—\_PrdV

‘ Mi

(67)

X_s = ^-\px-dV,y_s=±-\p.y.dV,z_s = ~\p-2-dV

M. y    Ax y    M. y

(6.8)