lastscan31

F

4000

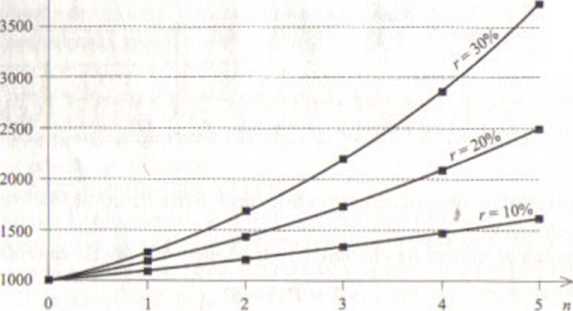
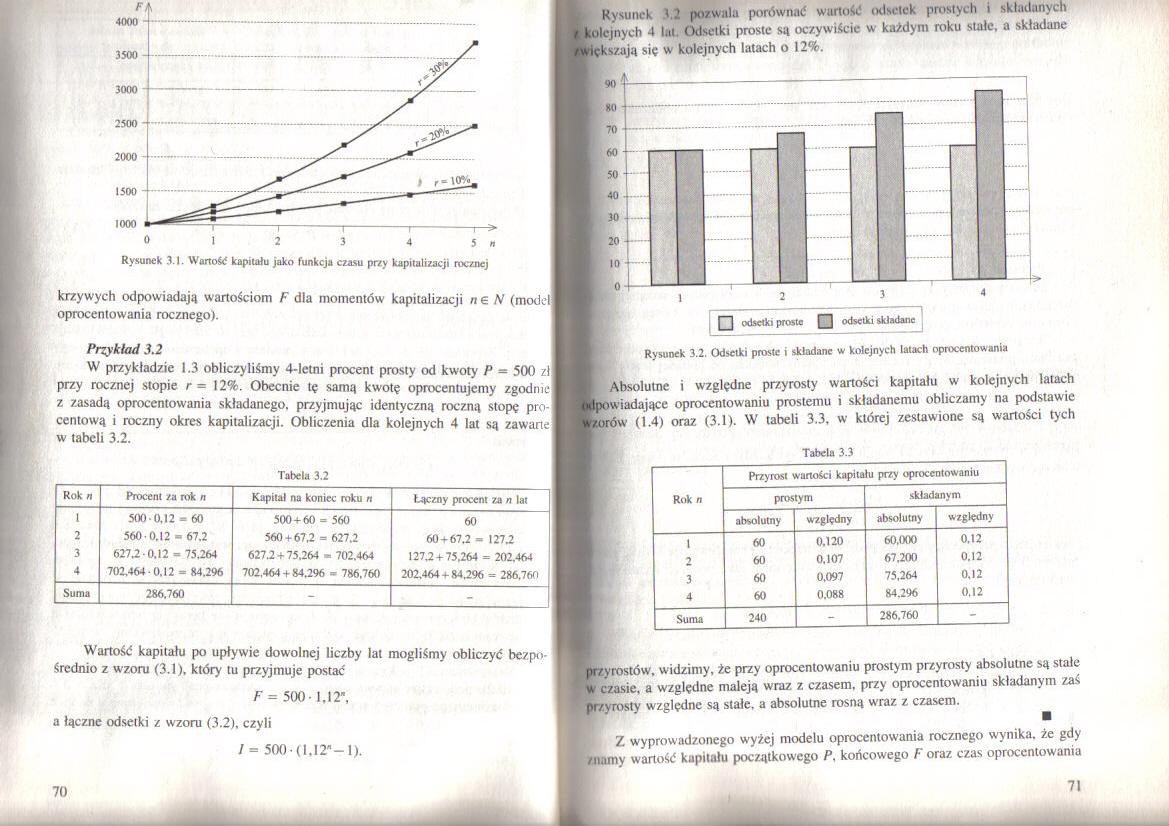
Rysunek 3.1. Wartość kapitału juko funkcja czasu przy kapitalizacji rocznej

krzywych odpowiadają wartościom F dla momentów kapitalizacji ne N (model oprocentowania rocznego).

Przykład 3.2

W przykładzie 1.3 obliczyliśmy 4-letni procent prosty od kwoty P = 500 zł I przy rocznej stopie r= 12%. Obecnie tę samą kwotę oprocentujemy zgodnie z zasadą oprocentowania składanego, przyjmując identyczną roczną stopę pro- f centową i roczny okres kapitalizacji. Obliczenia dla kolejnych 4 lat są zawarte w tabeli 3.2.

Tabela 3.2

Rok n	Procent za rok n	Kapitał na koniec roku n	Łączny procent za n lat
ł	500-0,12 - 60	500 + 60 - 560	60
2	560 0.12 - 67.2	560 + 67,2 = 627.2	60 + 67.2 - 127.2
3	627,2-0,12 - 75.264	627.2 + 75.264 - 702.464	127.2 + 75.264 = 202.464
4	702.464 -0.12 - 84.296	702.464 + 84.296 - 786.760	202.464 + 84.2% = 286.760
Suma	286.760	-

Wartość kapitału po upływie dowolnej liczby lat mogliśmy obliczyć bezpośrednio z wzoru (3.1). który tu przyjmuje postać

F= 500*1,12-,

a łączne odsetki z wzoru (3.2), czyli

/ = 500-(l.12"-1).

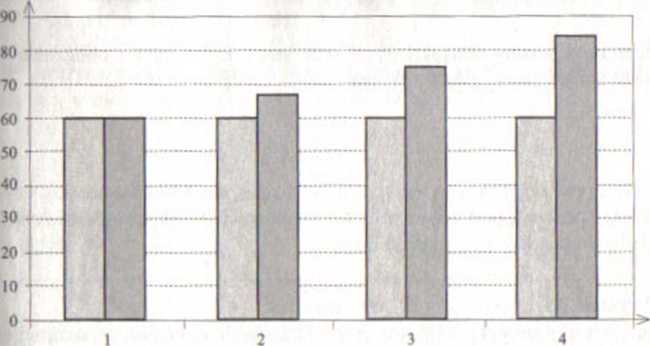
Rysunek 1 2 pozwala porównać wartość odsetek prostych i składanych ejnych 4 l.n Odsetki proste są oczywiście w każdym roku stałe, a składane tszają się w kolejnych latach o 12%.

□ odsetki proste    odsetki składane

Rysunek 3.2. Odsetki proste i składane w kolejnych latach oprocentowania

Absolutne i względne przyrosty wartości kapitału w kolejnych łatach nadające oprocentowaniu prostemu i składanemu obliczamy na podstawie w/.orów (1.4) oraz (3.1). W tabeli 3.3, w której zestawione są wartości tych

Tabela 3.3

Rok n	Przyrost wartości kapitału przy oprocentowaniu
	prostym		składanym
	absolutny	względny	absolutny	względny
\	60	0,120	60.000	0.12
2	60	0,107	67.200	0.12
3	60	0,097	75.264	0,12
4	60	0.088	84.296	0.12
Suma	240	-	286.760	-

—przyrostów, widzimy, że przy oprocentowaniu prostym przyrosty absolutne są stałe w czasie, a względne maleją wraz z czasem, przy oprocentowaniu składanym zaś

yrosty względne są stałe, a absolutne rosną wraz z czasem.

Z wyprowadzonego wyżej modelu oprocentowania rocznego wynika, że gdy znamy wartość kupilału początkowego P. końcowego F oraz czas oprocentowania

71