lastscan61

Czytelnikowi pozostawiamy sprawdzenie, że rozwiązując powyższy probl przy użyciu modelu (4.6). otrzymuje się

T o

oraz

T

o

K( 0) = J*(/)e-'*'d/,

przy czym równoważność stopy oprocentowania rocznego r oraz stopy oprcx towania ciągłego r_c gwarantuje otrzymanie w obu wariantach tych samych wam

K(D oraz K(0).

4.2. Zasada równoważności kapitałów

Zasada równoważności kapitałów jest jedną z najważniejszych zasad maten tyki finansowej. W rozdziale 5 będzie ona niezbędna do przeprowadzenia wyce renty. W' rozdziale 6 do budowy i analizy schematu spłaty długu, w rozdziale 7 konstrukcji mierników efektywności inwestycji, a w następnych rozdziała dotyczących inwestycji finansowych, do modelowania, wyceny i analizy inwestyi Punktem wyjścia rozważań jest następująca ogólna zasada równoważno kapitałów w momencie t.

Zasada równoważności kapitałów w momencie /

Kapitały i K₂ są równoważne w momencie /, jeśli ich wartości zaktualizowane na moment / są rów ne.

Od razu zauważamy, że w celu zbadania równoważności dwóch kapitałów trzebi po pierwsze, znać wartość każdego z nich w jakimkolwiek momencie, a f drugie - zaktualizować te wartości na wspólny moment t według wybranej modelu wartości kapitału.

W oparciu o powyższą zasadę wyprowadzimy formalny warunek równowai ności kapitałów K_] i K₂ w momencie /. aktualizując ich wartości według model wartości kapitału w czasie, wyprowadzonego w poprzednim punkcie rozdziału r podstawie zasady oprocentowania składanego. Przyjmujemy, że znana jest warto! Kj(fi) oraz wartość K₂(t2), przy czym A', (r,) > 0 oraz K₂(t₂) > 0. Przy użyci modelu (4.1) aktualizujemy wartość każdego kapitału na moment /, otrzymując

oraz

Kj</) = K₂(/₂)(l+rr^,ł.

równoważności kapitałów stanowi, że kapitały A', i A. mi równoważne

ncic t. jeśli spełniona jest równość A,(/) « A.(/), czyli jeśli

(4.10)

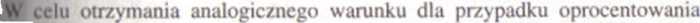
nie trzeba powtarzać całego wyprowadzenia - wystarczy w warunku zastąpić roczna stopę r równoważną stopą oprocentowania ciągłego r_c. sposób otrzymujemy warunek rów noważności o postaci

A,(r,)(l +r)'~'' = K₂(t₂)(\+r)-*. obustronnie powyższą równość przez (1 +r)^f. otrzymujemy warunek *■(0(1 +r)-'* = A₂(f₂)(l+r)-'Ł    (

MMe-'*'^{1 2} = A₂(/₂)e-'^

(4.11)

, badając równoważność kapitałów- A', i A₂ poprzez ich aktualizację na jt r. doszliśmy do warunku, w którym moment i nie występuje. A więc tfnle od wyboru momentu aktualizacji warunek równoważności kapitałów'² , n»a postać (4.10) lub (4.11). Wynika stąd następujący wniosek.

]i kapitały A, i A₂ równoważne w pewnym momencie /. to są także

równoważne w każdym momencie t' * t, i' e R.

formułowany wyżej wniosek jest bardzo ważny dlatego, że „uwalnia” relację ażności kapitałów- od czasu. Jeśli bowiem warunek równoważności w postaci lub (4.11) jest spełniony, to zamiast mówić, że kapitały A, i A₂ są ażne w dowolnym momencie t e R. mów imy po prostu, że są to kapitały ważne. Kapitały A, i A₂, które nie są równoważne, nazywamy kapitałami Równoważnymi. Łatwo można zauważyć, że w celu stwierdzenia nierów-OŚci kapitałów- A, i A₂ wystarczy sprawdzić, że nie są one równoważne jmkolwiek momencie t. Wobec tego w dalszych rozważaniach opartych na nlowaniu składanym możemy stosować zasadę równoważności kapitałów iłowaną w następujący sposób.

Zasada równoważności kapitałów itały A, i A, są równoważne, jeśli ich wartości zaktualizowane na jakikolwiek moment / e R są rów-ne.

131

1

_ W poprzednim punkcie rozdziału pokazaliśmy, że wartość funkcji Kit),

Klitce j modelem wartości w czasie kapitału K, oznacza wartość tego kapitału momencie t. Jednocześnie wiemy, że gdy kapitały A', i K₂ są równoważne, to ich •włości zaktualizowane na dowolny moment te R są równe. Wynika stąd. że funkcje A,(/) i A₂(/), będące modelami zmian wartości, odpowiednio, kapitału

2

A . przyjmują taką samą wartość dla każdego te R.