92� (2)

3. Rozpływy mocy

z faktu. Ze sieć jest słabo obciążona. Czytelnikowi pozostawia się uzasadnienie tego wyniku. W tablicy 3.4 podano obliczone napięcia węzłowe we współrzędnych prostokątnych i biegunowych, natomiast wyniki przepływów mocy w gałęziach i moce węzłowe pokazano na tys. 3.5.

Impcdancyjna metoda Gaussa

Macierz impedancyjną węzłową 2j,₇ dla rozpływów mocy tworzy się przez odwracanie macierzy admitancyjnej węzłowej dla modelu sieci w postaci dwójników. Wynika to z faktu, że macierz admitancyjna dla modelu czwómikowego sieci jest macierzą prawie osobliwą, gdyż wartości parametrów poprzecznych w czwómikach są o około rząd wielkości mniejsze od wartości parametrów podłużnych. W konsekwencji, parametry poprzeczne gałęzi skupia się w węzłach, tworząc admitancje poprzeczne węzłów y' , które przechodzą z modelu sieci (Z„₇ ) do modelu

obciążeń węzłowych jako źródła prądowe y'Ł/, (2.23) [21,23].

W dwójnikowym modelu sieci nie ma parametrów poprzecznych, a więc i węzła o potencjale zerowym (ziemi) jako węzła odniesienia. Węzeł bilansujący staje się jednocześnie węzłem odniesienia i macierz admitancyjna węzłowa o wymiarze (w - I) x (w 1) spełnia warunki odwra-calności. Problem ten szczegółowo jest omówiony w p. 3.2.5.

Wybierając punkt startowy do obliczeń w postaci wektora początkowych wartości napięć węzłowych , można wyliczyć prądy węzło-

we

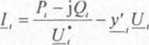
i = 1,2,...,w i*s

(3.20)

gdzic y' — admitancje poprzeczne (doziemne) w poszczególnych węzłach.

Nowe oszacowanie napięć uzyskuje się natomiast z impcdancyjnych równań węzłowych

(3.21)

Uw/. ^— Z |₎₇ /1,7 4- £/,

gdzie l/_t— wektor, którego wszystkie elementy są równe napięciu węzła bilansującego (odniesienia).

Z kolei obliczone napięcia węzłowe (3.21) można wykorzystać do ponownego obliczenia prądów węzłowych ze wzoru (3.20). Zarysowany schemat postępowania jest iteracyjną metodą Gaussa (3.12) z. wykorzystaniem macierzy impedancyjnej węzłowej Z_m. W metodzie tej prądy węzłowe (3.20) są ponownie obliczane po całkowitym zakończeniu poprzedniej iteracji, tj. wyliczeniu pełnego wektora napięć węzłowych (3.21).

Algorytm postępowania, w ogólnym przypadku, jest dwustopniowy. Napięcia węzłowe w kolejnych iteracjach oblicza się bezpośrednio ze wzoru

U',""' =U, + Y_JZ,_/L\^l)    i = 1,2.....w i*s (3.22)

/■i

gdzie Z,_y — element macierzy impedancyjnej węzłowej.

Drugim stopniem algorytmu jest obliczenie prądu węzłowego występującego we wzorze (3.22)

j=\,2,...,w j*s (3.23)

_/(t) ₌ ^PJ }Qj _ , „(*)

Impcdancyjna metoda Gaussa-Seidela

W metodzie tej schemat algorytmu jest identyczny jak w metodzie Gaussa, z tą różnicą, ż.c do funkcji iteracyjncj (3.22) podstawia się na bieżąco te wartości prądów    których napięcia węzłowe zostały obli-

* (*>

czone w iteracji k + 1. natomiast pozostałe prądy /_y są wyznaczone na podstawie napięć z. iteracji k. Jest to więc metoda Gaussa z relaksacyjnym prowadzeniem iteracji, pochodzącym z. relaksacyjnej metody Seidela rozwiązywania układu równań nieliniowych.

Równania na napięcia węzłowe są rozwiązywane w porządku określonym numerami węzłów

.....- i * s

J^mi

J*X

(3.24)

przy czym do obliczenia napięcia w kolejnym węźle i są wykorzystywane prądy węzłowe z. poprzedniej iteracji /**’ (dla j > i+1), obliczane podobnie jak poprzednio ze wzoru (3.23), lub uaktualniona wartość prądu /'/ *" (dla j < i 1), obliczana ze wzoru

93