Kolendowicz14

■ Największe naprężenie rozciągające w cięgnie obliczymy ze wzoru

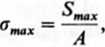
gdzie A jest polem przekroju poprzecznego cięgna.

■ Obliczenie długości cięgna nie przedstawia żadnych trudności. Można je wyznaczyć z prostych związków geometrycznych.

15.1.2. Punkty zawieszenia na różnych poziomach

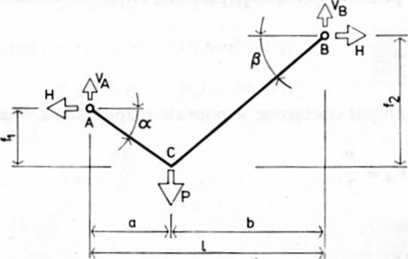
Reakcje i siły rozciągające cięgno o punktach zaczepienia nie leżących na tym samym poziomie (rys. 15-4) otrzymamy z równań podobnych jak dla cięgna, którego punkty zawieszenia znajdują się na jednym poziomie, mianowicie:

	ZPu = o.	Ha-Hb = 0,
stąd		Ha = Hb= //;	(15-15)
	ZP<r = 0,	VA+VB-P = 0,	(15-16)
	£ Mb = 0,	VAl+H(f2-f)-Pb = 0,
stąd		„ Pb — H(f2 —/i) /	(15-17)
	Z Mc — 0,	VAa-Hf =0,

stąd    V. = —.    (15-18)

a

Podstawiając wartość na V_A do równania (15-17) otrzymujemy

Hf,    Pb - H(f₂ -f_x)

a    I

stąd //= y[^a~.    (15-19)

fb +f₂a

■ Reakcję V_A obliczymy z równania (15-18), a mianowicie

314