matmaegzamni1

Egzammi pisemny z matematyki Wydział WILiŚ, Budownictwo, sem. 3, r.ak. 2008/2007

ZADANIA

Zad.Zl [6p - rozwiązanie piszemy na strOonie 1J

Obliczyć    moment bezwładności względem osi    OZ części jednorodnej kuli:

Z² + y² + Z²    < F? , a;    ^ 0, y > 0, 2 ^ 0    , (R > 0) , Q(x,y, z) =    po >    0.

Zad«Z2 [8p - rozwiązanie piszemy na stronie 2]

Obliczyć masę odcinka L o początku A(l_f2,3) i końcu £(0,2,2) , jeżeli gęstość masy dana jest wzorem g(x_ty,z) = x • y ‘ z.

Sprawdzić, że X —

3 '		1 3	0
1 0	jest wektorem własnym macierzy A =	0 2 0 0	-1 1 i

i znaleźć odpowiadającą

mu wartość własną macierzy A.

Zad.Z4 [12p - rozwiązanie piszemy na stronie 4]

co

£ (~l)ⁿ K-7 Je®* zbieżny, a następnie

_n=o 2n +1

Wyznaczyć zbiór tych wszystkich z e R > dla których szereg

wyznaczyć sumę tego ezeTegu. Ustalić rodzaj zbieżności.

Zad.Z5 [4p - rozwiązanie piszemy na stronie 5j Zmienna losowa X ma rozkład o dystrybuancie

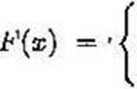
1-e-*

0

(<7 > 0) . Znaleźć a) gęstość zm. los. X , b) P(X > 1).

Zad.Z6 [7p - rozwiązanie piszemy na stronie 8)

Wynik pomiaru odległości jest obarczony błędem systematycznym b i błędem losowym X . Błąd systematyczny b = 60m i polega na podawaniu odległości większej niż rzeczywista. Błąd losowy jest zmienną o rozkładzie iV(0m; lOOm) . Podać rozkład zmiennej losowej błędu całkowitego, jego wartość oczekiwaną i odchylenie standartowe. Obliczyć p-stwo, że odczytany wynik pomiaru nie przekroczy prawdziwej odległości (skorzystać z tablic rozkładu normalnego).

Max. 38 pkt

TEORIA

Zad .Tl (4p - rozwiązanie piszemy na stronie 1]

1

Wykazać, że jeżeli liczba A jest wartością własną macierzy nieosobłiwej A , to liczba — jest wartością własną ₁    A

macierzy A ¹ .

Zad.T2 [6p - rozwiązanie piszemy na stronie 1]

co

n

b)

Podaj definicję zbieżności szeregu liczbowego. Sprawdź, czy dla szeregów a) £ (-3)ⁿ

na*l

co J

£ jest spełniony warunek konieczny zbieżności. Czy dane szeregi są zbieżne7

n=i vⁿ

Zad.T3 (3p - rozwiązanie piszemy na stronie 2]

Podać twierdzenie o różniczkowaniu szeregu potęgowego.

Zad.T4 [3p - rozwiązanie piszemy na stronie 2]

Zmienna losowa X ma rozkład Poissona z parametrem A = 3 . Przy pomocy tablic ustalić wartość dys trybu anty

m-

Zad.TS (6p - rozwiązanie piszemy na stronie 3]

Napisać tezę twierdzenia Lindberga-Levy’ego dla ciągu {Jć_n} niezależnych zmiennych losowych o tym samym rozkładzie jednostajnym

f 1    *6(0,1]

\0    **[0,11

/(*)

Dystrybuantę rozkładu normalnego standaryzowanego zapisać za pomocą całki.

Max. 22 pkt