Matma szereg funkcyjny cińÖgŕlszy 3

( 7 S> ‚Äúr". l^=ŇĀ U <Ňā
\y>-9wk^ \
c> o- ¬ę<
C^i if./.iC ;

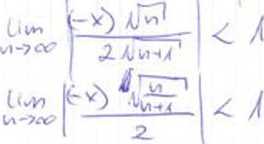
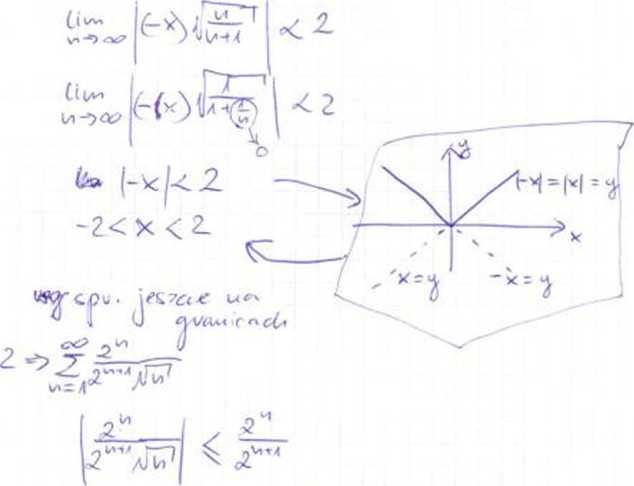
-4‚ÄĒ O' wir/
l*pC/
-2T *W*A ‚ÄĒ 9 sin
2
u¬Ľ
<w, _.n

-2" C& i*-?~< *j ‚ÄĒ^ 2?iMuńôUi X ‚ÄĒ ~ Z
‚Ė†^w ^ V^Ňā *~*J ^ C'
\jocLi in n. ‚ÄėyiO '^yno;^' '
T*^
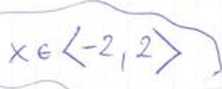
Wyszukiwarka
Podobne podstrony:
Matma szereg funkcyjny cińÖg?lszy 4 IŇā IŇā ¬ĽŇā IŇā *Ňā ?<? ?<f<f
Matma szereg funkcyjny cińÖg?lszy 5 (D 0 / ^ n> i/*r O.2 _ ¬ę
Matma szereg funkcyjny cińÖg?lszy fJ vV: <*r ńô - ; - jl * -i -.- ~y y V7Tk. at>..o-*i;
Matma szereg funkcyjny ŇõńÖegecfT Tomic fi ST* = ŇĀix *^‚Äú-eAi-e?u ńô>sw" Xz-t2h itr i , i_<
11014940?8343634532938437864211080361770 n II SZEREGI FUNKCYJNE ¬£/.(*). x&Xr<zR zbieŇľnoŇõńá pun
MATEMATYKA157 304 VI. CińÖgi i szeregt funkcyjne g) ¬£(sinx): n=Jj>h)Se‚Äú- 0 Z*‚ÄĚ
420 XII. CińÖgi i szeregi funkcyjne szereg ten jest zbieŇľny dla ‚ÄĒ 1 <x<. R√≥wnoŇõńá CO ¬£ (2x-x*)m
8 (18) 144 7. CińÖgi i szeregi funkcyjne f{e,l}) ‚ÄĒ ¬£ c‚Äěeinl> (9 - liczba rzeczywista). ¬Ľ-o Wtedy s
Definicja zbieŇľnoŇõci szeregu funkcyjnego IX) Szereg funkcyjny ¬£ /n(x) nazywamy zbieŇľnym w zbiorze X.
szeregi t-SSr ¬Ī¬£&r- ijw. ŇĽ<*>*. ¬ß¬Ľy.
kolos matma sem III (ŇĄ ) V 1 X N_? ;J ( ‚Ė†/w-C^oOwC^ ¬£ OjrCLvu.¬£ńÜ protM^,M¬£. jJ^-3)) (X > VVL
matma! IX <<s [X¬ę- a b x * ^t + b ¬£0 !_i C ¬£ C a ‚ÄĒ ‚ÄĒ _ ‚Ė†2 Q b J2c - cx. 57b PfH
matma 2 &&4i c*<rńá ńôuuuu <) ¬£**l4*"*k *$‚Ė†*-‚Äô*‚Ė† $*) > ‚Äė g-
matma sob z6 2 4 "Al £ i ^ i U Aj £ £- 4- / 4 V k
Rys. 23.2. Klucz szeregowy o zwińôkszonym tŇāumieniu Ňā‚ÄĒ¬į h¬įH3 -O * UWY 1 Rys. 23.3. Analogowy
wińôcej podobnych podstron