mech2 131

260

i

przy czym

= w oos a =

cos² a sic a ’

^uv

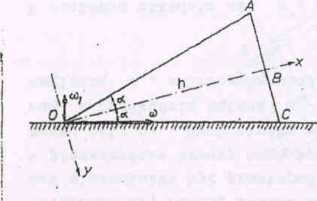
Ey3. 188

rnsina = u>^ oos a.

Momenty bezwładności stożka względem oai głównych x, y, wyznaczono w zadaniu 10 i 11, pkt 5.1

^Jxx = ⁿ ^ ^r2 =    ° ^h2 'Z²*’

T _ 3r² + 12h²    _ _l2 3tg²a + 12

^ ^{3 m} -20- = ^{D h} 20- •

Po podstawieniu otrzymamy*

^ m h² o>i sina,

K _{= B h}² _u 1 ,+ 3 ?°8²g .

^y 20 ^{w w} 1 cos a

Zadanie 2

Tarcza kołowa o promieniu r jest osadzona na wale o długości H. Wał jest umocowany na przegubie w punkcie 0 i obraca się wokół pionowej oai ze stałą prędkością u>>j. Zakłada jąo, że podczas ruchu tarcza toozy się bez poślizgu po płaszczyźnie poziomej, obliczyć naoisk tarczy na podłoże, Ciężar tarozy wynosi Q.

\z

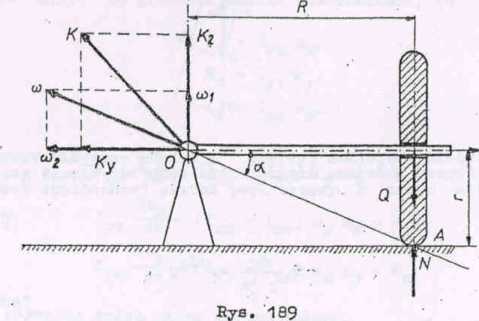
Rozwiązanie (rys. 189) i    ,•

Prędkość kątową w skierowaną wzdłuż chwilowej osi obrotu rozkładamy na - prędkość kątową precesji i Wg - prędkość kątową obrotu własnegd

0 . «

I

i

(0₂ = U)^ otg a = 0)^ —-

jjorzysfcamy z zasady laętu

dK.

W~ = V

f przyjętym na rys. 189 układzie osi (które są głównymi osiami bezwładności)

I

(bo u)^ =0)    ..

a czyli

**= ⁰

K = -I	|l]n ,
y 77	2 ^?
■ H II W	w* 1
z zz	1 ’
^Z *• V ”2 ^+	I „ u).. zz 1
oj^ i UJ2	są stałę

^rektorem o stałym module, obracającym się wokół osi z z prędkością ką-tową ^    ^

K = IF² = ^1 x K₀,

V^J0⁸V ^(Iyy “2 ^{+ r}zz “l^} = *yy ⁵1 ^X “2 ⁺    X g1?

O

ożyli

^ “1 * “a - ^Eo'

ClU X U)n = “bl ^

1 "2*

Moment sił zewnętrznych (tj. siły ciężkości i reakcji podłoża) względom punktu 0»

M₀ = » R - Q E,

r

stąd

Iyy “1 ^W2 " ~^QR>

I w. U)~

N = -23— -S + Q.

Moment bezwładnośoi tarczy względem osi y:

V =" ^ - &^l2-