mech2 143

284

= m g (b - J_an) + D,

®P

przy czym h - wysokość położenia płaszczyzny półkuli nad poziomem    •:

mi,

7_Sp “ odległość środka ciężkości pręta od płaszczyzny półkuli 1 (w położeniu poozątkowym),

D - potencjał na poziomie ziemi.

W położeniu końcowym

1 r ...2

^B2 = -t'*o “ ’

U₂ = m g (h - y_sk) + D,

przy czym    “ odległość środka ciężkości pręta od płaszczyzny półkuli ■!

(w położeniu końcowym), '

1^    - moment bezwładności pręta względem osi poziomej przecho

dzącej przez środek kuli,

Zadanie 9

285

■ ya² -1²',

sp

^xo = ^xs ⁺ “y

sk’

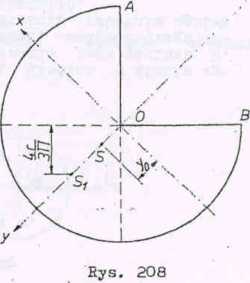
Przekrój walca o ciężarze G ma postać trzech czwartych koła o promieniu r.- Waleo może obracać się wokół osi przechodzącej przez punkt 0. Promieniowi OA nadano położenie pionowe, a następnie pozostawiono walec Aacrn w>nemetim rHe^.nrowi. Jaka na.lwieksza prędkość osiągnie punkt A.

jego własnemu ciężarowi. Jaką największą prędkość osiągnie punkt

Eozwiązanie (rys. 208)

Korzystamy z zasady równoważności pracy i energii kinetycznej

^Xo ⁼ * T5 ⁺ “

: = ^ (ja² - 2i²).

Między prędkością liniową końców pręta i prędkością kątową zachodzi zvrią- | zek

i*

PodstBwiająo m , I_o, y_ak, y_sp do równania wynikającego z zasady zachowania energii otrzymamy po uproszczeniu

¥

5gd Cd - 1) Yći² -

“5-T

3& - 21*

iię ,² -o

2 g d mas

^{= ay}o(- y

vf)

Należy znaleźć położenie środka ciężkości przekroju waloa. Środek musi Ij leżeć na 03i symetrii przekroju y, wyznaczamy odległość y_Q od osi x

y 3s =    s + 0 • s + 0

^y ) K^r

przy cżym s — pole jednej ćwiartki koła, ^! stąd •

o 9 u

3 Podstawiając do równania wynikającego z zasady równoważności pracy i *■*

; nergii kinetycznej otrzymamy

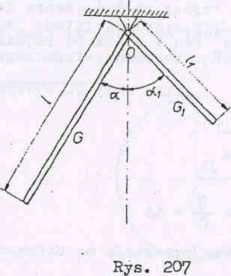
^x Zadanie 8 (rys. 207)

Dwa jednorodne pręty o ciężarach G i 5., oraz długościach 1 i L są | * Wynika stąd, umocowane obrotowo w punkcie O. Odchylamy pręty o kąty a i    od poło- J

żenią pionowego, a następnie puszczamy. Jaka powinna być zależność między kątami b I , aby pręty osiągając położenie pionowe miały jednakową energię kinetyczną.

16gr

tr.ax

4

9rr

( V2 - 1),

Odp.

sin

= fj/f ( VF- -o'

“1

sin -g-

\

A