mech2 127

253

252

253

252

przy czym

I

r_ = a,

1*

2X] + x = const.

a = g

"2- ^Q2

6eo^c

a =    —2

b^d + 6o

.2

S = G

o + 6c

Z •

^sr

T _ ^Q2 ^r2

^X2 - T ? •

Równania ruchu krążka ruchomego (ruch płaski):

o r²

^T1 ^E1 '= g T^{- E}1 = ^S2 ^T1 " ^S1 ^r1

ą*

g ^B1 ⁼ ^1 ’ ^S1 ” ^S2*

Między przyspieszeniami zachodzą związki

2 2 ^E1 ^r1 ⁼

Ponadto należy zauważyć, że długość sznura jest stała, czyli

2Xyj + 3

Różniozkując ten związek otrzymamy

2Xj + x = 0 ,

przy czym czyli

2a^ = a.

Z równań więzów i równań ruchu ciężaru oraz krążków: stałego i ruchomego moglibyśmy wyznaczyć niewiadome S, , S₂, e^, a, a^. Interesujące nas wielkość a wyrazi się za pomocą zadanych ciężarów następująco:

^Q~

Zadanie 3 (rys. 100)

Na krążek 1 o promieniu R i oiężarze Q, mogący obracać się wokół po-ziome-j osi przechodzącej przez jego środek ciężkości, została nawinięta nić, a drugi jej koniec został nawinięty na krążek 2 o ciężarze G i promieniu r. Wyznaczyć przyspieszenie środka ciężkości krążka 2 spadającego pod działaniem siły ciężkości.

Odp. a= Zadanie 4

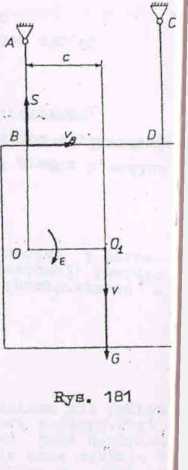
Jednorodna kwadratowa płyta o ciężarze G i boku b je9t zawieszona w dwu punktach B i D swego górnego poziomego boku na dwóch pionowyob cięgnach. Wyznaczyć, jak wielkie napięcie będzie w pierwszej chwili ^ł cięgnie AB, gdy cięgno CD zostaje przecięte.

Rozwiązanie (rys. 181)

Płyta będzie poruszać się ruohem płaskim. Środek ohwilonego obrotu 0 'znajdziemy wiedząc, że prędkość punktu B będzie prostopadła do AB,a pręd

i kość środka płyty będzie miała kierunek pionowy.

'2

* Równanie ruohu środka masy będzie następująoe ma = E P,

| stąd rzut na pion |    - a = G - S.

I

| Bównanie dynamiczne ruohu obrotowego wokół ohwi-I iowego środka obrotu

I₀e=* G o,

j przy czym I_Q - moment bezwładności względem osi prostopadłej do płyty w punkcie 0

i *. ■ s⁺1 °²-

przy czym I_Q - moment bezwładnośoi względem osi

^ prostopadłej do płyty w punkcie 0^.

2

t G b^

S ⁼ T w •

Podatawiająo do równania dynamicznego a= ta mamy

^G 0 = -f (V ⁺ °²) ^ '

stąd

a następnie

s

Zadanie 5

Jednorodna-płyta trójkątna ABC, o bakach AB = 30, BC = 2c i£ ABC = n/2, jest zawieszona w narożnikach A i B u& dwóch pionowych oięgnaa Następnie cięgno BF przecięto. Porównać napięcie w cięgnie AR przed pr cięoiem i w obwili przeoięcia.

Odp. ^il ^—

Zadanie 6 (rys. 182)

Kula i waleo, połączone prętem AB jak na rysunku 182, staozają s z równi pochyłej, nachylonej do poziomu pod kątem a . Obliozyć siłę po stającą w pręoie AB oraz przyspieszenie z jakim układ ten będzie stacz się z równi, jeżeli oiężary kuli i walca Bą równe Q,a promienie obu oi są równe r.