mech2 119

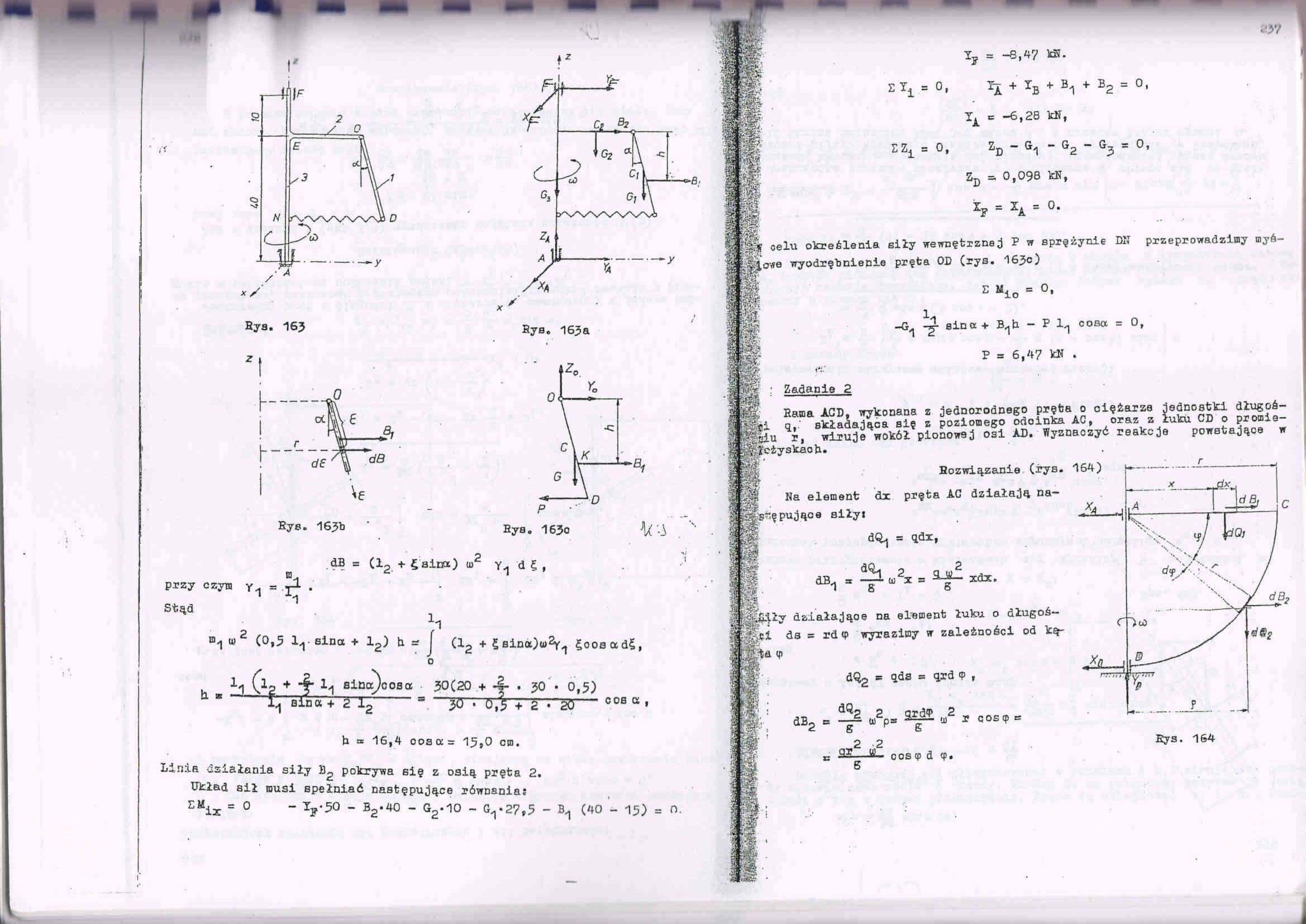
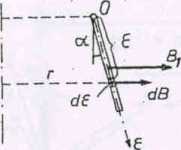
Bya. 163

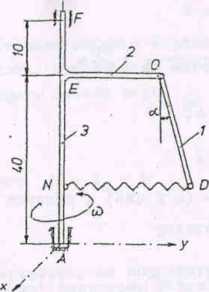
Bys. 163a

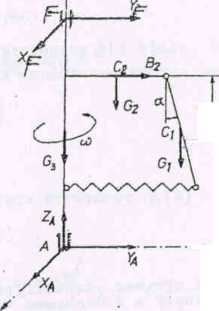
Bys. 163b

dB = (1₂ + £aina) uf y^ d £ ,

przy czym y . = yl .

¹ 1

Stąd

^X1

ⁿ1 u) ² (°»5 sina + 1₂) h =r j (l₂ + ę sina)^^ ęoos ad£,

o

0*2 ⁺ "f* L-j sina)co8a 30(20 +    . 30 • 0,5)

^ “    Ł, sin a + 2 1₂    ⁼    30 • 0,5 + 2 • 20 ^{C0B a} *

b » 16,4 oosa= 15,0 cm.

Linia działania siły łU pokrywa się z osią pręta 2.

Układ sił musi spełniać następujące równania?

EM_ix =0    - Ty*50 - B₂-40 - G₂-10 ~ G^-27,5 - B₁ (40 - 15)

■ y/

sz. = o,

dQ₂ = <łds = qrd <p ,

^d*2    2 qrd<P ,2

2 -2

c H£—^— costp d cp»

E 1 j = O ,

dQ^ = qdi,

Ty = -8,47 kH.

^XA ^{+ X}B ⁺ B1 ⁺ B2 = °*

I_A = -6,28 kN,

Z_D -    “ ^G2 - ^G3 ⁼ O*

Z_D =. 0,098 kN,

I_F = Z_A = 0.

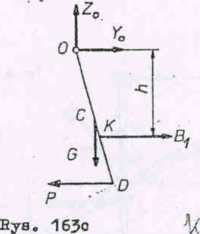
oelu określenia siły wewnętrznej P w sprężynie DN przeprowadzimy myś-ovre wyodrębnienie pręta OD (rys. 1630

E M_io = O,

-G^ sina + B^b - P 1^ cosa = O,

P = 6,47 kN .

<"•

Zadanie 2

Rama ACD, wykonana z jednorodnego pręta o ciężarze jednostki długoś-i q,.' składająca się z poziomego odcinka AC, oraz z luku CD o promie-’u r, wiruje wokół pionowej osi AD. Wyznaczyć reakcje powstające w eżyskaotu

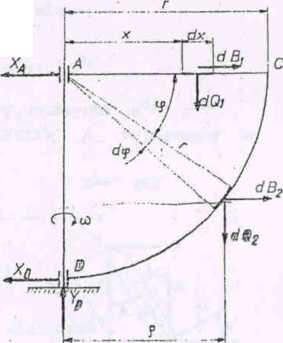
Eys. 164

Rozwiązanie (irys. 164)

Na element dr pręta AC działają następujące siłyi

^^IdI-

$ły działająoe na element łuku o długości da = rd «P wyrazimy w zależności od ką-ia <p

i